题目内容
（2011?安徽模拟）“嫦娥二号”卫星于2010年10月1日发射成功，它经过三次近月制动后，在近月轨道上做匀速圆周运动（运动半径可看作月球半径）．若地球质量为M，半径为R，第一宇宙速度为ν；月球半径为r，质量为m．则“嫦娥二号”在近月轨道上运动的速度大小为（ ）
分析：根据万有引力提供向心力，通过地球的第一宇宙速度求出万有引力常量，再根据万有引力提供向心力求出嫦娥二号在近月轨道上的速度．
解答：解：月球给嫦娥二号的万有引力提供向心力，有：G
=m0
，解得v′=
．
因为地球的第一宇宙速度为v，有G
=m′
，解得G=
．
所以v′=
?v．故B正确，A、C、D错误．
故选B．
| mm0 |
| r2 |
| v′2 |
| r |
|
因为地球的第一宇宙速度为v，有G
| Mm′ |
| R2 |
| v2 |
| R |
| v2R |
| M |
所以v′=
|
故选B．
点评：解决本题的关键知道第一宇宙速度等于贴近星球表面做匀速圆周运动的速度，会通过万有引力提供向心力求解线速度的大小．
练习册系列答案
科学实验活动册系列答案
相关题目
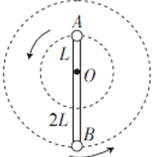（2011?安徽模拟）如图所示，轻杆长为3L，在杆的A、B两端分别固定质量均为m的球A和球B，杆上距球A为L处的点O装在光滑的水平转动轴上，外界给予系统一定的能量后，杆和球在竖直面内转动．在转动的过程中，忽略空气的阻力．若球B运动到最高点时，球B对杆恰好无作用力，则下列说法正确的是（ ）
（2011?安徽模拟）如图所示为大型电子地磅电路图，电源电动势为E，内阻不计．不称物体时，滑片P到A端，滑动变阻器接入电路的有效电阻最大，电流较小；称重物时，在压力作用下使滑片P下滑，滑动变阻器有效电阻变小，电流变大，这样把电流对应的重量值刻在刻度盘上，就可以读出被称物体的重量值，若滑动变阻器上A、B间距离为L，最大阻值等于电阻阻值R0，已知两只弹簧的总弹力与形变量成正比，其比例系为k，所称重物的重量G与电流大小I的关系为（ ）
（2011?安徽模拟）如图所示，有一足够长斜面，倾角α=37°，一小物块质量为m，从斜面顶端A处由静止下滑，到B处后，受一与物体重力大小相等的水平向右恒力作用，开始减速，到C点减速到0（C点未画出）．若AB=225m．物块与斜面间动摩擦因素μ=0.5，sin37°=0.6，cos37°=0.8，g=10m/s2．
（2011?安徽模拟）如图是某中学科技小组制作的利用太阳能驱动小车的装置．当太阳光照射到小车上方的光电板，光电板中产生的电流经电动机带动小车前进．若射到小车上方的光电板，光电板中产生的电流经电动机带动小车前进．若小车在平直的水泥路上从静止开始加速行驶，经过时间t前进距离s，速度达到最大值vm，设这一过程中电动机的功率恒为P，小车所受阻力恒为F，那么（ ）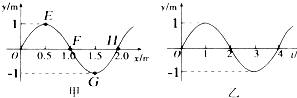
（2011?安徽模拟）一列沿着x轴正方向传播的横波，在t=2s时刻的波形如图甲所示，则图乙表示图甲中E、F、G、H四个质点中，哪一质点的振动图象（ ）