题目内容
如图所示,质量相等的三个物块A、B、C,A与天花板之间、B与C之间均用轻弹簧相连,A与B之间用细绳相连,当系统静止后,突然剪断AB间的细绳,则此瞬间三物块的加速度分别为aA= ,aB= ,aC= (取向下为正).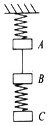
【答案】分析:根据胡克定律弹力F=kx,和力和运动剪断细绳的瞬间,绳的弹力立即消失,面这一瞬间弹簧的形变量没有发生变化而弹簧弹力不变,进而根据牛顿第二定律分析加速度情况.
解答:解:抓住剪断绳的瞬间,绳的弹力立即消失,而弹簧弹力瞬间不变,所以分析:
对A受力分析有:
剪断前平衡有:F=mg+F绳 ①
剪断瞬间:a=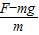 =
=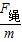 ; ②
; ②
对B进行受力分析有:
剪断前平衡有:F绳=mg+F弹BC ③
剪断瞬间有:a=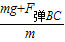 ④
④
对C进行受力分析有:
剪断前平衡:F弹BC=mg ⑤
剪断瞬间: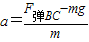 ⑥
⑥
由⑤⑥知C的加速度为0;
把⑤代入④得B的加速度a=2g,方向向下
把⑤和③代入②得A的加速度大小为2g,方向向上
因为取向下为正方向
故答案为:-2g,2g,0
点评:题是力学中的瞬时问题,关键是先根据平衡条件求出各个力,然后根据牛顿第二定律列式求解加速度;同时要注意轻弹簧的弹力与行变量成正比,来不及突变,而细线的弹力是有微小形变产生的,故可以突变.
解答:解:抓住剪断绳的瞬间,绳的弹力立即消失,而弹簧弹力瞬间不变,所以分析:
对A受力分析有:
剪断前平衡有:F=mg+F绳 ①
剪断瞬间:a=
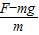 =
=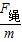 ; ②
; ②对B进行受力分析有:
剪断前平衡有:F绳=mg+F弹BC ③
剪断瞬间有:a=
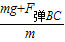 ④
④对C进行受力分析有:
剪断前平衡:F弹BC=mg ⑤
剪断瞬间:
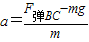 ⑥
⑥由⑤⑥知C的加速度为0;
把⑤代入④得B的加速度a=2g,方向向下
把⑤和③代入②得A的加速度大小为2g,方向向上
因为取向下为正方向
故答案为:-2g,2g,0
点评:题是力学中的瞬时问题,关键是先根据平衡条件求出各个力,然后根据牛顿第二定律列式求解加速度;同时要注意轻弹簧的弹力与行变量成正比,来不及突变,而细线的弹力是有微小形变产生的,故可以突变.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 如图所示,质量相等的物体A和物体B与地面间的动摩擦因数相等,在力F的作用下,一起沿水平地面向右移动x,则( )
如图所示,质量相等的物体A和物体B与地面间的动摩擦因数相等,在力F的作用下,一起沿水平地面向右移动x,则( )| A、摩擦力对A、B做功不相等 | B、A、B动能的增量相同 | C、F对A做的功与F对B做的功相等 | D、合外力对A做的功与合外力对B做的功相等 |
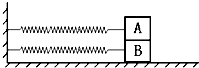 如图所示,质量相等的物块A、B叠放在光滑水平面上.两轻质弹簧的一端固定在竖直墙壁上,另一端分别与A、B相连接.两弹簧的原长相同,与A相连的弹簧的劲度系数小于与B相连的弹簧的劲度系数.开始时A、B处于静止状态.现对物块B施加一水平向右的拉力,使A、B一起向右移动到某一位置又处于静止状态(A、B无相对滑动,弹簧处于弹性限度内),撤去这个拉力后( )
如图所示,质量相等的物块A、B叠放在光滑水平面上.两轻质弹簧的一端固定在竖直墙壁上,另一端分别与A、B相连接.两弹簧的原长相同,与A相连的弹簧的劲度系数小于与B相连的弹簧的劲度系数.开始时A、B处于静止状态.现对物块B施加一水平向右的拉力,使A、B一起向右移动到某一位置又处于静止状态(A、B无相对滑动,弹簧处于弹性限度内),撤去这个拉力后( )| A、A受到的合力总等于弹簧对B的弹力 | B、A受到的合力总大于弹簧对B的弹力 | C、A受到的摩擦力始终与弹簧对它的弹力方向相同 | D、A受到的摩擦力与弹簧对它的弹力方向有时相同,有时相反 |
 如图所示,质量相等的五个物块在光滑水平面上,间隔一定距离排成一条直线.具有初动能E0的物块1向其它4个静止的物块运动,依次发生碰撞,每次碰撞后不再分开.最后5个物块粘成一个整体.这个整体的动能等于( )
如图所示,质量相等的五个物块在光滑水平面上,间隔一定距离排成一条直线.具有初动能E0的物块1向其它4个静止的物块运动,依次发生碰撞,每次碰撞后不再分开.最后5个物块粘成一个整体.这个整体的动能等于( ) (2011?罗湖区模拟)如图所示,质量相等的甲、乙两物体位于同一水平线上的A、B两点.甲作平抛运动,同时乙作自由落体运动.AC为甲的运动轨迹,BC为乙的运动轨迹,两轨迹相交于C点,(空气阻力忽略,两物体距离地面足够高)则两物体( )
(2011?罗湖区模拟)如图所示,质量相等的甲、乙两物体位于同一水平线上的A、B两点.甲作平抛运动,同时乙作自由落体运动.AC为甲的运动轨迹,BC为乙的运动轨迹,两轨迹相交于C点,(空气阻力忽略,两物体距离地面足够高)则两物体( )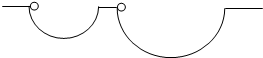 半径为r和R(r<R)的光滑半圆形槽,其圆心均在同一水平面上,如图所示,质量相等的两物体分别自半圆形槽左边缘的最高点无初速地释放,在下滑过程中两物体( )
半径为r和R(r<R)的光滑半圆形槽,其圆心均在同一水平面上,如图所示,质量相等的两物体分别自半圆形槽左边缘的最高点无初速地释放,在下滑过程中两物体( )