题目内容
火车以速度v1匀速行驶,司机发现前方同轨道上相距s处有另一火车沿同方向以速度v2(对地且v1>v2)做匀速直线运动.司机立即以加速度a紧急刹车.要使两车不相撞,a应满足什么条件?
解析:
|
【解答】此题有多种解法. 解法1 两车运动情况如图所示,后车刹车后虽做匀减速运动,但在其速度减小至和v2之前两车的距离仍将逐渐减小,当后车速度减小至小于前车速度,两车距离将逐渐增大.可见,当两车速度相等时,两车距离最近.若后车减速的加速度过小,则会出现后车速度减为和前车速度相等之前即追上前车,发生撞车事故;若后车加速度过大,则会出现后车速度减为和前车速度相等时仍未追上前车,根本不可能发生撞车事故;若后车加速度大小为某值时,恰能使两车在速度相等时后车追上前车,这正是两车恰不相撞的临界状态,此时对应的加速度即为两车不相撞的最小加速度.综上分析可知,两车恰不相撞时应满足下列两方程:
v1t- v1-a0t=v2 ② 解之可得:a0= 所以当a≥ 解法2 要使两车不相撞,其位移关系应为
v1t- 即
对任一时间t,不等式都成立的条件为 Δ=(v2-v1)2-2as≤0, 由此得
a≥ 解法3 以前车为参照物,刹车后后车相对前车做初速度v0=v1-v2、加速度为a的匀减速直线运动.当后车相对前车的速度减为零时,若相对位移 得
a≥ 【评析】三种解法中,解法一注重对运动过程的分析,抓住两车间距离有极值时速度应相等这一关键条件来求解;解法二中由位移关系得到一元二次方程,然后利用根的判别式来确定方程中各系数间的关系,这也是中学物理中常用的数学方法;解法三通过巧妙地选取参照物,使两车运动的关系变得简明. |
提示:
|
【分析】在追及问题中,可利用两者位移关系建立方程,此题中两者位移满足S1+=S+S2时追上. |

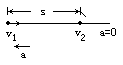
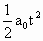 =v2t+s ①
=v2t+s ①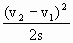
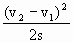 时,两车即不会相撞.
时,两车即不会相撞.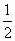 at2≤s+v2t
at2≤s+v2t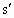 ≤s,则不会相撞,故由
≤s,则不会相撞,故由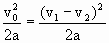 ≤s,
≤s,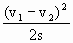 .
. (2012?广东一模)2011年7月23日晚,雷雨交加,两列同向行驶的列车,行经浙江省温州市鹿城区黄龙街道双岙村下岙处路段高架桥面时,突然相撞--D301次动车快速追尾D3115次动车,6节车厢脱轨,3节坠落桥下(如图).在这次事故中,180余名受伤旅客成功获救,但仍有40人在这次特大铁路交通事故中遇难.事故引发公众对公共安全的高度关注.高三的小丁根据新闻进行了如下思考:火车A以对地速度v1匀速行驶,司机发现正前方同一轨道上相距s处有另一火车B沿同方向以对地速度v2(v2<v1)做匀速运动,A车司机立即以加速度a(绝对值)紧急刹车,为使两车不相撞,请求出a应满足什么条件?
(2012?广东一模)2011年7月23日晚,雷雨交加,两列同向行驶的列车,行经浙江省温州市鹿城区黄龙街道双岙村下岙处路段高架桥面时,突然相撞--D301次动车快速追尾D3115次动车,6节车厢脱轨,3节坠落桥下(如图).在这次事故中,180余名受伤旅客成功获救,但仍有40人在这次特大铁路交通事故中遇难.事故引发公众对公共安全的高度关注.高三的小丁根据新闻进行了如下思考:火车A以对地速度v1匀速行驶,司机发现正前方同一轨道上相距s处有另一火车B沿同方向以对地速度v2(v2<v1)做匀速运动,A车司机立即以加速度a(绝对值)紧急刹车,为使两车不相撞,请求出a应满足什么条件? 2011年7月23日晚,雷雨交加,两列同向行驶的列车,行经浙江省温州市鹿城区黄龙街道双岙村下岙处路段高架桥面时,突然相撞--D301次动车快速追尾D3115次动车,6节车厢脱轨,3节坠落桥下(如图).在这次事故中,180余名受伤旅客成功获救,但仍有40人在这次特大铁路交通事故中遇难.事故引发公众对公共安全的高度关注.高三的小丁根据新闻进行了如下思考:火车A以对地速度v1匀速行驶,司机发现正前方同一轨道上相距s处有另一火车B沿同方向以对地速度v2(v2<v1)做匀速运动,A车司机立即以加速度a(绝对值)紧急刹车,为使两车不相撞,请求出a应满足什么条件?
2011年7月23日晚,雷雨交加,两列同向行驶的列车,行经浙江省温州市鹿城区黄龙街道双岙村下岙处路段高架桥面时,突然相撞--D301次动车快速追尾D3115次动车,6节车厢脱轨,3节坠落桥下(如图).在这次事故中,180余名受伤旅客成功获救,但仍有40人在这次特大铁路交通事故中遇难.事故引发公众对公共安全的高度关注.高三的小丁根据新闻进行了如下思考:火车A以对地速度v1匀速行驶,司机发现正前方同一轨道上相距s处有另一火车B沿同方向以对地速度v2(v2<v1)做匀速运动,A车司机立即以加速度a(绝对值)紧急刹车,为使两车不相撞,请求出a应满足什么条件?