题目内容
某小组用如图甲所示装置“验证牛顿第二定律”空车质量为200g,另有多个质量为100g的砝码用以改变小车质量.将细线一端拴上连有纸带的小车,另一端跨过定滑轮拴质量为l0g的钩码,利用打点计时器(频率为50Hz)打出的纸带,测出5组对应不同小车质量的加速度a,测得的数据记录在表乙中.木板水平且很光滑.
表乙
(1)某同学借用以上数据测定重力加速度.他已将记录的数据整理后标在图丙所示坐标纸上,请你在坐标纸上作出相应图线,并根据图线求得当地重力加速度的测量值为g= m/s2
(2)试分析说明图线不过坐标原点的原因.
(3)当小车质量为500g时对应的纸带如图丁所示(打A点时小车刚好运动,相邻的计数点间还有四个点未画出),该同学用这条纸带验证机械能守恒定律.由静止释放钩码至打点E时,钩码的重力势能损失 J,系统的动能增加 J(查得当地重力加速度g=9.8m/s2,保留两个有效数字)

表乙
| 砝码的质量m/g | 10 | ||||
| 小车的质量M/g | 200 | 300 | 400 | 500 | 600 |
| 加速度a/(m?s-2) | 0.452 | 0.306 | 0.232 | 0.187 | 0.156 |
(2)试分析说明图线不过坐标原点的原因.
(3)当小车质量为500g时对应的纸带如图丁所示(打A点时小车刚好运动,相邻的计数点间还有四个点未画出),该同学用这条纸带验证机械能守恒定律.由静止释放钩码至打点E时,钩码的重力势能损失

分析:(1)根据坐标系中描出的点作出图象,然后由图象求出重力加速度.
(2)应用牛顿第二定律求出
-
的函数表达式,然后分析答题.
(3)由EP=mgh求出小车重力势能的损失;根据做匀变速直线运动的物体在某段时间内的平均速度等于该段时间中间时刻的瞬时速度求出E点的瞬时速度,然后求出小车的动能.
(2)应用牛顿第二定律求出
| 1 |
| a |
| M |
| m |
(3)由EP=mgh求出小车重力势能的损失;根据做匀变速直线运动的物体在某段时间内的平均速度等于该段时间中间时刻的瞬时速度求出E点的瞬时速度,然后求出小车的动能.
解答: 解:(1)根据坐标系中所描出的点作出图象,图象如图所示;
解:(1)根据坐标系中所描出的点作出图象,图象如图所示;
小车与钩码组成的系统,由牛顿第二定律得:mg=(M+m)a,
解得:
=
+
,由此可知:
-
图象斜率的倒数等于重力加速度,
由图象可知:k=
=
=0.1,重力加速度g=
=
=10m/s2.
(2)小车与钩码组成的系统,由牛顿第二定律得:mg=(M+m)a,
解得:
=
+
,由
=
+
可知,
-
图象不过原点,
在坐标轴上的截距为
,只有当m<<M,
趋向于无穷大时,
与
才近似成正比,本实验不满足该条件,因此图象不过原点.
(3)打点E时,钩码的重力势能损失EP=mghAE=0.01kg×9.8m/s2×0.3357m≈0.033J;
计数点间的时间间隔t=0.02s×5=0.1s,打E点时小车的速度vE=
=
=0.1815m/s,
打E点时动能的增加量EK=
mvE2=
×0.5×0.18152≈0.0032.
故答案为:(1)图象如图所示;10;(2)没有满足m<<M;(3)0.033;0.032.
 解:(1)根据坐标系中所描出的点作出图象,图象如图所示;
解:(1)根据坐标系中所描出的点作出图象,图象如图所示;小车与钩码组成的系统,由牛顿第二定律得:mg=(M+m)a,
解得:
| 1 |
| a |
| 1 |
| g |
| 1 |
| g |
| M |
| m |
| 1 |
| a |
| M |
| m |
由图象可知:k=
△
| ||
△
|
| 6.4-0.4 |
| 60-0 |
| 1 |
| k |
| 1 |
| 0.1 |
(2)小车与钩码组成的系统,由牛顿第二定律得:mg=(M+m)a,
解得:
| 1 |
| a |
| 1 |
| g |
| 1 |
| g |
| M |
| m |
| 1 |
| a |
| 1 |
| g |
| 1 |
| g |
| M |
| m |
| 1 |
| a |
| M |
| m |
在坐标轴上的截距为
| 1 |
| g |
| M |
| m |
| 1 |
| a |
| M |
| m |
(3)打点E时,钩码的重力势能损失EP=mghAE=0.01kg×9.8m/s2×0.3357m≈0.033J;
计数点间的时间间隔t=0.02s×5=0.1s,打E点时小车的速度vE=
| DF |
| 2t |
| 0.3720m-0.3357m |
| 2×0.1s |
打E点时动能的增加量EK=
| 1 |
| 2 |
| 1 |
| 2 |
故答案为:(1)图象如图所示;10;(2)没有满足m<<M;(3)0.033;0.032.
点评:要掌握描点法作图的方法,应用牛顿第二定律求出加速度倒数
与
的表达式是正确解题的关键.
| 1 |
| a |
| M |
| m |

练习册系列答案
 中考解读考点精练系列答案
中考解读考点精练系列答案
相关题目
(Ⅰ)一物理兴趣小组利用学校实验室的数字实验系统探究物体作圆周运动时向心力与角速度、半径的关系.
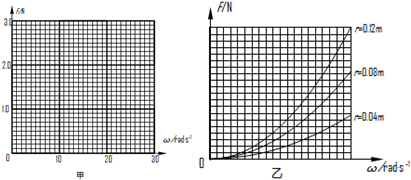
①首先,他们让一砝码做半径r为0.08m的圆周运动,数字实验系统通过测量和计算得到若干组向心力F和对应的角速度ω,如下表.请你根据表中的数据在图甲上绘出F-ω的关系图象.

②通过对图象的观察,兴趣小组的同学猜测F与ω2成正比.你认为,可以通过进一步转换,做出______关系图象来确定他们的猜测是否正确.
③在证实了F∝ω2之后,他们将砝码做圆周运动的半径r再分别调整为0.04m、0.12m,又得到了两条F-ω图象,他们将三次实验得到的图象放在一个坐标系中,如图乙所示.通过对三条图象的比较、分析、讨论,他们得出F∝r的结论,你认为他们的依据是______.
④通过上述实验,他们得出:做圆周运动的物体受到的向心力F与角速度ω、半径r的数学关系式是F=kω2r,其中比例系数k的大小为______.(计算结果取2位有效数字)
(Ⅱ)某同学想测量某导电溶液的电阻率,先在一根均匀的长玻璃管两端各装了一个电极(接触电阻不计),两电极相距L=0.700m,其间充满待测的导电溶液.
用如下器材进行测量:
电压表(量程l5V,内阻约30kΩ); 电流表(量程300μA,内阻约50Ω);
滑动变阻器(10Ω,1A); 电池组(电动势E=12V,内阻r=6Ω);
单刀单掷开关一个、导线若干.
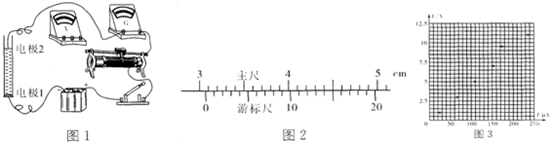
下表是他测量通过管中导电液柱的电流及两端电压的实验数据.实验中他还用20分度的游标卡尺测量了玻璃管的内径,结果如图2所示

根据以上所述请回答下面的问题:
(1)玻璃管内径d的测量值为______mm;
(2)根据表1数据在图3坐标中已描点,请作出U-I图象,根据图象求出电阻R=______Ω(保留两位有效数字);
(3)计算导电溶液的电阻率表达式是ρ=______ 4L
| 实验序号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| F/N | 2.42 | 1.90 | 1.43 | 0.97 | 0.76 | 0.50 | 0.23 | 0.06 |
| ω/rad?s-1 | 28.8 | 25.7 | 22.0 | 18.0 | 15.9 | 13.0 | 8.5 | 4.3 |

②通过对图象的观察,兴趣小组的同学猜测F与ω2成正比.你认为,可以通过进一步转换,做出______关系图象来确定他们的猜测是否正确.
③在证实了F∝ω2之后,他们将砝码做圆周运动的半径r再分别调整为0.04m、0.12m,又得到了两条F-ω图象,他们将三次实验得到的图象放在一个坐标系中,如图乙所示.通过对三条图象的比较、分析、讨论,他们得出F∝r的结论,你认为他们的依据是______.
④通过上述实验,他们得出:做圆周运动的物体受到的向心力F与角速度ω、半径r的数学关系式是F=kω2r,其中比例系数k的大小为______.(计算结果取2位有效数字)
(Ⅱ)某同学想测量某导电溶液的电阻率,先在一根均匀的长玻璃管两端各装了一个电极(接触电阻不计),两电极相距L=0.700m,其间充满待测的导电溶液.
用如下器材进行测量:
电压表(量程l5V,内阻约30kΩ); 电流表(量程300μA,内阻约50Ω);
滑动变阻器(10Ω,1A); 电池组(电动势E=12V,内阻r=6Ω);
单刀单掷开关一个、导线若干.
下表是他测量通过管中导电液柱的电流及两端电压的实验数据.实验中他还用20分度的游标卡尺测量了玻璃管的内径,结果如图2所示
| U/V | 1.0 | 3.0 | 5.0 | 7.0 | 9.0 | 11.0 | |
| I/μA | 22 | 65 | 109 | 155 | 175 | 240 |

根据以上所述请回答下面的问题:
(1)玻璃管内径d的测量值为______mm;
(2)根据表1数据在图3坐标中已描点,请作出U-I图象,根据图象求出电阻R=______Ω(保留两位有效数字);
(3)计算导电溶液的电阻率表达式是ρ=______ 4L


 mvb2-
mvb2- mva2,计算重物重力势能的减少量mgh,比较它们的大小是否相等.
mva2,计算重物重力势能的减少量mgh,比较它们的大小是否相等.
