题目内容
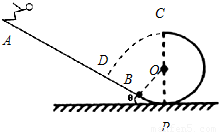
质量m=50kg的跳台花样滑雪运动员（可看成质点），从静止开始沿斜面雪道从A点滑下，沿切线从B点进入半径R=15m的光滑竖直冰面圆轨道BPC，通过轨道最高点C水平飞出，经t=2s落到斜面雪道上的D点，其速度方向与斜面垂直．斜面与水平面的夹角θ=37°，运动员与雪道之间的动摩擦因数μ=0.075，不计空气阻力．取当地的重力加速度g=10m/s2，sin37°=0.60，cos37°=0.80．试求：（1）运动员运动到C点时的速度大小vC；
（2）运动员在圆轨道最低点P受到轨道支持力的大小FP；
（3）A点到过P点的水平地面的高度h．
【答案】分析：运动员从C点到D点做平抛运动，在D点对速度进行分解解得平抛的初速度．
根据机械能守恒定律求得P点时的速度大小，根据牛顿第二定律解得受到轨道支持力的大小．
解答：解：（1）运动员从C点到D点做平抛运动，在D点对速度进行分解，
根据运动的分解得：
得：vC=gttanθ
代入数据解得vC=15m/s
（2）设运动员运动到P点时的速度大小为vP，根据机械能守恒定律得：
，
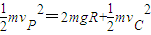根据牛顿第二定律得：
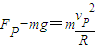
联立解得：FP=3250N
（3）根据动能定理研究从A点到P点有：
联立解得：h=45.5m
答：（1）运动员运动到C点时的速度大小是15m/s；
（2）运动员在圆轨道最低点P受到轨道支持力的大小是3250N；
（3）A点到过P点的水平地面的高度是45.5m．
点评：高考中对于力学基本规律考查的题目一般都设置了多个过程，要灵活选择物理过程利用所学的物理规律求解．
根据机械能守恒定律求得P点时的速度大小，根据牛顿第二定律解得受到轨道支持力的大小．
解答：解：（1）运动员从C点到D点做平抛运动，在D点对速度进行分解，
根据运动的分解得：
得：vC=gttanθ
代入数据解得vC=15m/s
（2）设运动员运动到P点时的速度大小为vP，根据机械能守恒定律得：
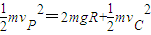，根据牛顿第二定律得：
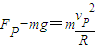
联立解得：FP=3250N
（3）根据动能定理研究从A点到P点有：
联立解得：h=45.5m
答：（1）运动员运动到C点时的速度大小是15m/s；
（2）运动员在圆轨道最低点P受到轨道支持力的大小是3250N；
（3）A点到过P点的水平地面的高度是45.5m．
点评：高考中对于力学基本规律考查的题目一般都设置了多个过程，要灵活选择物理过程利用所学的物理规律求解．
练习册系列答案
相关题目
如图所示，质量m=50kg的跳水运动员从距水面高h=10m的跳台上以30°角斜向上跳出，初速度v0=5m/s，最终落入水中．若忽略运动员的身高和空气阻力．取g=10m/s2，求：
（2010?连城县模拟）如图所示，质量m=50kg的跳水运动员从距水面高h=10m的跳台上以v0=5m/s的速度斜向上起跳，最终落入水中．若忽略运动员的身高．取g=10m/s2，求：
（2013?北京）蹦床比赛分成预备运动和比赛动作．最初，运动员静止站在蹦床上；在预备运动阶段，他经过若干次蹦跳，逐渐增加上升高度，最终达到完成比赛动作所需的高度；此后，进入比赛动作阶段．
如图所示，质量m=50kg的跳水运动员从距水面高h=10m的跳台上以v0=5m/s的速度斜向上起跳，最终落入水中．若忽略运动员的身高和空气阻力的影响．（以水面为参考平面）取g=10m/s2，求运动员：