题目内容
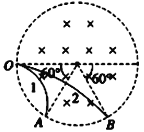
【题目】如图所示,扇形AOB为透明柱状介质的横截面,折射率为![]() ,OM为∠AOB的角平分线,M为一点光源,从M发出的一束平行于OB的光线由C点折射后的折射光线平行于OM。光在真空中的速度为c,求:
,OM为∠AOB的角平分线,M为一点光源,从M发出的一束平行于OB的光线由C点折射后的折射光线平行于OM。光在真空中的速度为c,求:
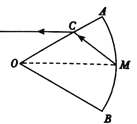
①∠AOB的大小;
②若OC的距离为L,求光在该透明介质中的传播时间。
【答案】(1) ![]() (2)
(2) ![]()
【解析】试题分析:作出光路图,根据几何关系和折射定律即可求出∠AOB的大小;求出出光传播的距离和速度即可求出光在该透明介质中的传播时间。
①设![]() ,光线的入射角
,光线的入射角![]() ,折射角为
,折射角为![]() ,过C点做OA的垂线交OM于D点,根据几何关系可得:
,过C点做OA的垂线交OM于D点,根据几何关系可得: ![]()
根据折射定律有: ![]()
解得: ![]()

②因为:∠AOM=30°,∠CDO=60°,![]() ,所以∠CMO=30°
,所以∠CMO=30°
所以CM=OC=L
光在介质中的速度为: ![]()
运动时间为: ![]()
解得: ![]()

练习册系列答案
 轻松夺冠全能掌控卷系列答案
轻松夺冠全能掌控卷系列答案
相关题目