��Ŀ����
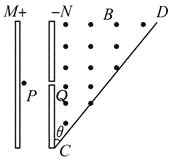
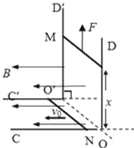
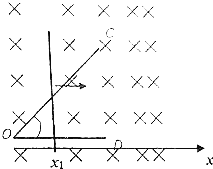
����Ŀ����ͼ��ˮƽ������һ���ϡ��⻬��������COD�����費�ƣ�![]() ���㹻��ֱ��������ڵ����ϣ���λ���ȵĵ���Ϊr=0.5�����������ֱOD���ռ���ڴ�ֱ�ڵ���ƽ��Ĵų�����O��Ϊԭ����OD�����������ᣬ�����x��0һ�������x�������������Ⱥ�ų����仯��Ϊ0.5T/m��O��Ÿ�Ӧǿ��B0=1T�������������£�����һ���ij��ٶ�������ֱ���˶����˶�ʱ��·�еĵ���ǿ�ȱ��ֲ��䡣��֪�˶���ͼ��x1=1mλ��ʱ���ٶȴ�Сv1=2m/s�����·�еĵ���ǿ�ȴ�СΪ__A����x1=1mλ���������˶�1m�Ĺ����У�ͨ��������ĵ���Ϊ__C��
���㹻��ֱ��������ڵ����ϣ���λ���ȵĵ���Ϊr=0.5�����������ֱOD���ռ���ڴ�ֱ�ڵ���ƽ��Ĵų�����O��Ϊԭ����OD�����������ᣬ�����x��0һ�������x�������������Ⱥ�ų����仯��Ϊ0.5T/m��O��Ÿ�Ӧǿ��B0=1T�������������£�����һ���ij��ٶ�������ֱ���˶����˶�ʱ��·�еĵ���ǿ�ȱ��ֲ��䡣��֪�˶���ͼ��x1=1mλ��ʱ���ٶȴ�Сv1=2m/s�����·�еĵ���ǿ�ȴ�СΪ__A����x1=1mλ���������˶�1m�Ĺ����У�ͨ��������ĵ���Ϊ__C��
���𰸡�6 3.5
��������
[1]����ɵã�![]() λ�ôŸ�Ӧǿ�ȣ�
λ�ôŸ�Ӧǿ�ȣ�
![]()
�������Ч���и�ȣ�
![]()
����������ĸ�Ӧ�綯�ƣ�
![]()
��·�еĵ��裺
![]()
��ŷķ���ɵã���·�еĵ���ǿ�ȴ�С��
![]()
[2]���ƶ���![]() λ��
�![]()
�ڼ���ʱ����t�ڲ����ĵ�����
![]()
��ʱ![]() �Ĵ�СΪ��
�Ĵ�СΪ��
![]()
![]() ��
��![]()
����R�Ĵ�С![]()
����������ĸ�Ӧ�綯��Ϊ��
![]()
��Ӧ������
![]()
����
![]()
![]()
�ɵã�
![]()
����
![]()

��ϰ��ϵ�д�
 ͨ��ѧ��Ĭд����ϵ�д�
ͨ��ѧ��Ĭд����ϵ�д� ���ƽ̸�������ѡ����ĩ���100��ϵ�д�
���ƽ̸�������ѡ����ĩ���100��ϵ�д�
�����Ŀ