题目内容
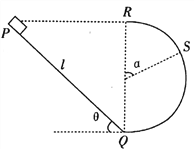
【题目】下图是用传送带传送行李的示意图。图中水平传送带AB间的长度为8m，它的右侧是一竖直的半径为0.8m的1/4圆形光滑轨道，轨道底端与传送带在B点相切。若传送带向右以6m/s的恒定速度匀速运动，当在传送带的左侧A点轻轻放上一个质量为4kg的行李箱时，箱子运动到传送带的最右侧如果没被捡起，能滑上圆形轨道，而后做往复运动直到被捡起为止。已知箱子与传送带间的动摩擦因数为0.1，重力加速度大小为g=10m/s2，求：
⑴箱子从A点到B点所用的时间及箱子滑到圆形轨道底端时对轨道的压力大小；
⑵若行李箱放上A点时给它一个5m/s的水平向右的初速度，到达B点时如果没被捡
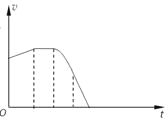
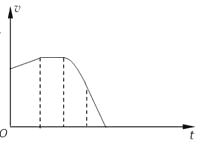
起，则箱子离开圆形轨道最高点后还能上升多大高度？在给定的坐标系中定性画出箱子从A点到最高点过程中速率v随时间t变化的图象。
【答案】（1）
（2）
【解析】试题分析：（1）皮带的速度
箱子的加速度
=1m/s2（2分）
设箱子在B点的速度为
，
（1分）
（1分）
所以箱子从A点到B点一直做匀加速运动：
（1分）
解得从A点到B点运动的时间为
（1分）
箱子在圆形轨道最低点时
（2分）
解得：
（1分）
由牛顿第三定律知箱子对轨道的压力大小为（1分）
（2）设箱子速度达到时位移为
，则
（1分）
解得
（1分）
因此箱子先匀加速运动一段时间，速度达到6m/s后
开始做匀速运动，即在B点的速度为
由机械能守恒定律
（2分）
解得高度（1分）
图象如图（3分）
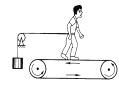
名师点睛字词句段篇系列答案
【题目】探究力对原来静止的物体做的功与物体获得速度的关系的实验装置如图所示。
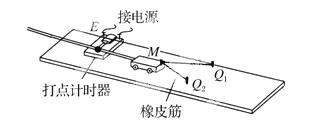
(1）下列说法正确的是：
A．通过改变橡皮筋的条数改变拉力做功的数值 |
B．通过改变橡皮筋的长度改变拉力做功的数值 |
C．通过打点计时器打下的纸带来测定小车加速过程中获得的最大速度 |
D．通过打点计时器打下的纸带来测定小车加速过程中获得的平均速度 |
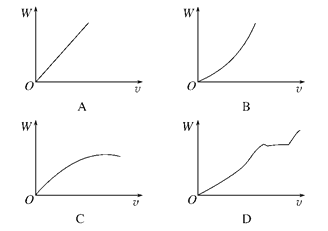
(2）通过实验获得较科学的数据作出的W－v图象，应为图中的哪一个：
