题目内容
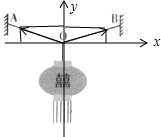
 如图为春节悬挂灯笼的一种方式,A、B点等高,O为结点,轻绳AO、BO长度相等,绳子对O点拉力分别为FA、FB,灯笼受到的重力为G,下列表述不正确的是( )
如图为春节悬挂灯笼的一种方式,A、B点等高,O为结点,轻绳AO、BO长度相等,绳子对O点拉力分别为FA、FB,灯笼受到的重力为G,下列表述不正确的是( )分析:以O点为研究对象作出受力分析图,由正交分解法可得出平行四边形,由几何关系可得出各力间的关系.
解答:解:设∠AOB=2θ,O点受到FA、FB、F三力作用,其中F=G,建立如图所示的坐标系,
列平衡方程得:
FAsinθ=FBsinθ
FAcosθ+FBcosθ=G
解出:
FA=FB=
;
则可知,两绳的拉力一定相等,故A正确;
本题选不正确的,故选B.

列平衡方程得:
FAsinθ=FBsinθ
FAcosθ+FBcosθ=G
解出:
FA=FB=
| G |
| 2cosθ |
则可知,两绳的拉力一定相等,故A正确;
本题选不正确的,故选B.
点评:本题由于两力的夹角不确定,故用合成法较为麻烦,因此本解法采用了正交分解法,可以轻松构造出直角三角形,则能顺利得出角边的关系.

练习册系列答案
相关题目

