��Ŀ����
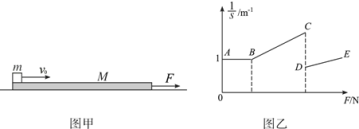
����Ŀ����ͼ����ʾ������ΪM=0��5kg��ľ�徲ֹ�ڹ⻬ˮƽ���ϣ�����Ϊm=1kg������Գ��ٶ�v0=4m/s����ľ�����ˣ������ľ��֮��Ķ�Ħ������Ϊ��=0��2������黬��ľ���ͬʱ����ľ��ʩ��һ��ˮƽ���ҵĺ���F��������Fȡijһֵʱ�������ľ���������ľ�廬����·��Ϊs����ľ��ʩ�Ӳ�ͬ��С�ĺ���F���õ�![]() �Ĺ�ϵ��ͼ����ʾ������AB�����ƽ�У���AB�ε�������Ϊ1m��1���������Ϊ�ʵ㣬���Ħ�������ڻ���Ħ�������������ٶ�g=10m/s2��
�Ĺ�ϵ��ͼ����ʾ������AB�����ƽ�У���AB�ε�������Ϊ1m��1���������Ϊ�ʵ㣬���Ħ�������ڻ���Ħ�������������ٶ�g=10m/s2��
��1��������F=0���������ľ����Ҷ˻��£��������ľ���ϻ��е�ʱ���Ƕ��٣�
��2��ͼ����BCΪֱ�߶Σ���öκ���F��ȡֵ��Χ��![]() ������ϵʽ��
������ϵʽ��
���𰸡���1��![]() ��2��
��2��![]()
���������Գ��ٶ�v0Ϊ�������������������ֻ�������Ħ��������ţ�ٵڶ����ɣ�![]()
���ļ��ٶȴ�СΪ��![]()
��ľ���У�![]() ľ���ļ��ٶȴ�СΪ��
ľ���ļ��ٶȴ�СΪ��![]()
��tʱ��������λ��Ϊ��![]() ľ���λ��Ϊ��
ľ���λ��Ϊ��![]()
���ǵ�λ�ƹ�ϵΪ��![]() ��ͼ��֪���峤L=1m
��ͼ��֪���峤L=1m
�����ϴ������ݿɽ�ã�![]()
![]()
��t=1sʱ��������ٶ�Ϊ2m/s��ľ����ٶ�Ϊ4m/s����������ľ���Ҷ˻���ʱ��������ٶȲ�����С��ľ����ٶ���![]() Ӧ������������ʱ��Ϊ
Ӧ������������ʱ��Ϊ![]() ��
��
��2���ٵ�F��Сʱ����齫��ľ���Ҷ˻��£���F����ijһֵʱ���ǡ�õ���ľ����Ҷˣ������߾��й�ͬ�ٶ�v����ʱt1������ľ���У�![]()
�����ٶ���ͬ��![]() ����λ��Ϊ��
�������![]()
ľ���λ��Ϊ��![]() λ�Ƽ�Ĺ�ϵΪ��
λ�Ƽ�Ĺ�ϵΪ��![]()
������ϵ��![]() ��ͼ���֪��
��ͼ���֪��![]() ��ã�
��ã�![]()
�ڵ�F��������ʱ�������١�ľ����٣�������ľ����ijһλ�þ��й�ͬ�ٶȣ������߹��ٺ��ܱ�����Ծ�ֹ����Ħ�������ã�һ������ͬ���ٶ�a4���ȼ����˶���
����������![]() �������
�������![]()
��fΪ��Ħ���������㣺 f��fmax=��mg=2N ������������ã�F��3N
����������BC�κ���F��ȡֵ��Χ��1N��F��3N��������ϵʽ��![]() ��
��