题目内容
如图甲所示,一宽度为L且足够长的光滑“匚”形金属导轨水平放置在匀强磁场中,匀强磁场的磁感应强度为B,方向竖直向下,“匚”形金属导轨上连接一阻值为R的电阻.一质量为m长为L的导体棒,刚好横跨在导轨上.现导体棒在水平恒力F作用下从静止开始向右运动,当棒获得某一最大速度时立即撤掉水平恒力F.设导体棒始终与导轨接触并且不分离,导轨和金属杆的电阻不计.

(1)求出棒的加速度a和速度v的关系式,并分析棒的运动情况.
(2)当撤掉水平恒力F后,求系统产生的电能.
(3)在图乙上画出棒的a-v图线.(要求标上有关坐标)

(1)求出棒的加速度a和速度v的关系式,并分析棒的运动情况.
(2)当撤掉水平恒力F后,求系统产生的电能.
(3)在图乙上画出棒的a-v图线.(要求标上有关坐标)
分析:(1)本题要求加速度与速度的关系,应从分析受力入手,则法拉第定律、欧姆定律、安培力公式推导出安培力与速度的关系,再根据牛顿第二定律列式求得加速度与速度的关系式,就可以分析棒的运动情况.
(2)当棒获得最大速度时,加速度a=0,由上题结果求出最大速度.当撤掉水平恒力F后,棒做减速运动,最终棒的动能全部转化为系统的电能,由能量守恒列式求得电能.
(3)根据前面的结论,作出图象.
(2)当棒获得最大速度时,加速度a=0,由上题结果求出最大速度.当撤掉水平恒力F后,棒做减速运动,最终棒的动能全部转化为系统的电能,由能量守恒列式求得电能.
(3)根据前面的结论,作出图象.
解答:解:(1)选向右方向为正,当水平恒力F作用时,导体棒两端的感应电动势为E=BLv
则流过导体棒的感应电流为I=
导体棒受到的安培力:F安=BIL
根据牛顿第二定律有:F-F安=ma
联立上式可得:a=
-
当撤掉水平恒力F后a=-
棒的运动情况是先做加速度减小的加速运动,后做加速度减小的减速运动.
(2)当棒获得最大速度时,即有a=0
则有
=
则得v=
系统产生的电能Q=
mv2=
(3)a与v是线性关系.如图所示.

答:
(1)棒的加速度a和速度v的关系式为:撤去F前,a=
-
;当撤掉水平恒力F后a=-
.棒的运动情况是先做加速度减小的加速运动,后做加速度减小的减速运动.
(2)当撤掉水平恒力F后,系统产生的电能为
.
(3)在图乙上画出棒的a-v图线如图所示.
则流过导体棒的感应电流为I=
| E |
| R |
导体棒受到的安培力:F安=BIL
根据牛顿第二定律有:F-F安=ma
联立上式可得:a=
| F |
| m |
| B2L2v |
| mR |
当撤掉水平恒力F后a=-
| B2L2v |
| mR |
棒的运动情况是先做加速度减小的加速运动,后做加速度减小的减速运动.
(2)当棒获得最大速度时,即有a=0
则有
| F |
| m |
| B2L2v |
| mR |
则得v=
| FR |
| B2L2 |
系统产生的电能Q=
| 1 |
| 2 |
| mF2R2 |
| 2B4L4 |
(3)a与v是线性关系.如图所示.

答:
(1)棒的加速度a和速度v的关系式为:撤去F前,a=
| F |
| m |
| B2L2v |
| mR |
| B2L2v |
| mR |
(2)当撤掉水平恒力F后,系统产生的电能为
| mF2R2 |
| 2B4L4 |
(3)在图乙上画出棒的a-v图线如图所示.
点评:本题中安培力是联系加速度与速度的桥梁,要能根据法拉第定律、欧姆定律等等规律推导出安培力与速度的关系,难度适中.

练习册系列答案
 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案 普通高中同步练习册系列答案
普通高中同步练习册系列答案
相关题目
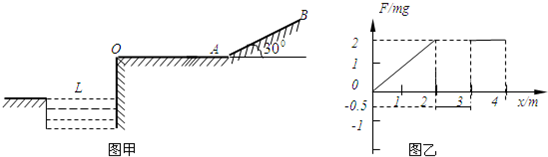


 的足够长光滑斜面AB在A处用一小段光滑圆弧相连,一质量为m的滑块从O处由静止开始受一水平力作用(力向右为正),F只在水平面上按图乙所示的规律变化,O点左侧有一水池,O点高出水面,滑块与水平面间的动摩擦因数为
的足够长光滑斜面AB在A处用一小段光滑圆弧相连,一质量为m的滑块从O处由静止开始受一水平力作用(力向右为正),F只在水平面上按图乙所示的规律变化,O点左侧有一水池,O点高出水面,滑块与水平面间的动摩擦因数为 ,
, ,求:
,求: