题目内容
 如图所示,在水平向右的匀强电场中,一根长为L的绝缘细线,一端连着一质量为m带电量为+q的小球,另一端固定于O点,现把小球拉至细线水平且与场强方向平行的位置,无初速释放,小球能摆到最低点的另一侧,细线与竖直方向的最大夹角θ=30°,(1)求场强E的大小;(2)若使带电小球在平行于电场的竖直平面内做完整的圆周运动,小球运动过程中的最小动能是多少?
如图所示,在水平向右的匀强电场中,一根长为L的绝缘细线,一端连着一质量为m带电量为+q的小球,另一端固定于O点,现把小球拉至细线水平且与场强方向平行的位置,无初速释放,小球能摆到最低点的另一侧,细线与竖直方向的最大夹角θ=30°,(1)求场强E的大小;(2)若使带电小球在平行于电场的竖直平面内做完整的圆周运动,小球运动过程中的最小动能是多少?分析:小球在运动的过程中,重力和电场力做功,初末的动能都是0,代人动能定理的表达式,即可求出得出强度;
当细线上张力为零时,重力和电场力的合力充当向心力,此时小球速度最小.
当细线上张力为零时,重力和电场力的合力充当向心力,此时小球速度最小.
解答:解:(1)对小球运动的全过程列动能定理方程:mgLcosθ-qEL(1+sinθ)=0,θ=30°,
解得E=
(2)当细线上张力为零时,重力和电场力的合力充当向心力,此时小球速度最小:
F合=
=
mg=
,
则Ek=
mv2=
mgL
答:(1)场强E的大小
;
(2)若使带电小球在平行于电场的竖直平面内做完整的圆周运动,小球运动过程中的最小动能是
mgL.
解得E=
| ||
| 3q |
(2)当细线上张力为零时,重力和电场力的合力充当向心力,此时小球速度最小:
F合=
| (mg)2+(qE)2 |
2
| ||
| 3 |
| mv2 |
| L |
则Ek=
| 1 |
| 2 |
| ||
| 3 |
答:(1)场强E的大小
| ||
| 3q |
(2)若使带电小球在平行于电场的竖直平面内做完整的圆周运动,小球运动过程中的最小动能是
| ||
| 3 |
点评:该题考查动能定理的应用,在做题的过程中要找出那些力做功,做了多少功;初末的状态分别是怎样的.
求解最小速度时关键是先找出在何处有最小速度.
求解最小速度时关键是先找出在何处有最小速度.

练习册系列答案
 考前必练系列答案
考前必练系列答案
相关题目
 如图所示,在水平向右的匀强电场中,用长为L的绝缘细绳将一个质量为m的带电小球悬挂于O点,平衡时,小球位于B点,此时绳与竖直方向的夹角为θ(θ<45°).已知重力加速度为g.求:
如图所示,在水平向右的匀强电场中,用长为L的绝缘细绳将一个质量为m的带电小球悬挂于O点,平衡时,小球位于B点,此时绳与竖直方向的夹角为θ(θ<45°).已知重力加速度为g.求: 如图所示,在水平向右的拉力F作用下,木块在长木板上向右做匀减速直线运动,加速度大小为a.长木板处于静止状态.已知,木块质量为m,长木板质量为M,长木板与水平地面间的动摩擦因数为μ1,木块与长木板间的动摩擦因数为μ2.地面对长木板的摩擦力大小为( )
如图所示,在水平向右的拉力F作用下,木块在长木板上向右做匀减速直线运动,加速度大小为a.长木板处于静止状态.已知,木块质量为m,长木板质量为M,长木板与水平地面间的动摩擦因数为μ1,木块与长木板间的动摩擦因数为μ2.地面对长木板的摩擦力大小为( ) 如图所示,在水平向右的匀强电场中,用长为L的绝缘细绳将一个质量为m的带电小球悬挂于O点,平衡时,小球位于B点,此时绳与竖直方向的夹角为θ(θ<45°).已知重力加速度为g.求:小球静止在B点时受到绳的拉力大小.
如图所示,在水平向右的匀强电场中,用长为L的绝缘细绳将一个质量为m的带电小球悬挂于O点,平衡时,小球位于B点,此时绳与竖直方向的夹角为θ(θ<45°).已知重力加速度为g.求:小球静止在B点时受到绳的拉力大小. 如图所示,在水平向右场强为E的匀强电场中,有一质量为m、电荷量为+q的点电荷从A点由静止释放,在电场力的作用下经时间t运动到B点.求:
如图所示,在水平向右场强为E的匀强电场中,有一质量为m、电荷量为+q的点电荷从A点由静止释放,在电场力的作用下经时间t运动到B点.求: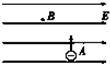 如图所示,在水平向右的匀强电场中的A点,有一个质量为m、带电荷量为-q的油滴以速度v竖直向上运动.已知当油滴经过最高点B时,速度大小也为v.求:
如图所示,在水平向右的匀强电场中的A点,有一个质量为m、带电荷量为-q的油滴以速度v竖直向上运动.已知当油滴经过最高点B时,速度大小也为v.求: