题目内容
一列简谐波沿直线传播，A、B、C是直线上的三点，如图所示，某时刻波传到B点，A刚好位于波谷，已知波长大于3m小于5m，AB=5m，周期T=0.1s，振幅A=5cm，再经过0.5s，C第一次到达波谷，求：（1）A、C相距多远？（2）到此时为止，A点运动的路程为多大？
【答案】分析：根据题给条件，分析A、B两点状态的关系，结合波形，得到AB距离与波长的关系通项式，根据波长大于3m小于5m，AB=5m，确定波长的值．由波传播的距离x=vt求出AC间的距离及A运动路程．
解答：解：（1）若AB=（n+
）λ，
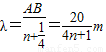，（n=0.1，2，、、、）
由于3m＜λ＜5m，则n取1，得到λ=4m，v=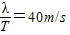
AC=vt+λ=（40×0.5+4）m=24m
若AB=（n+
）λ，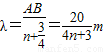
＜3m，故不符合题意．
（2）AB距离为5m，波长为4m，则波传到B点时A已振动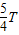
时间．
则A点运动的路程S=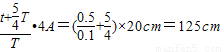
=1.25m
答：（1）A、C相距24m．
（2）到此时为止，A点运动的路程为1.25m．
点评：本题关键要考虑空间的周期性，列出距离与波长关系的通项式．通过分析推理，深刻理解波动的本质，培养运用数学知识解决物理问题的能力．
解答：解：（1）若AB=（n+
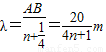）λ，，（n=0.1，2，、、、）由于3m＜λ＜5m，则n取1，得到λ=4m，v=
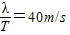
AC=vt+λ=（40×0.5+4）m=24m
若AB=（n+
）λ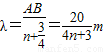，＜3m，故不符合题意．（2）AB距离为5m，波长为4m，则波传到B点时A已振动
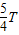时间．则A点运动的路程S=
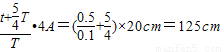=1.25m答：（1）A、C相距24m．
（2）到此时为止，A点运动的路程为1.25m．
点评：本题关键要考虑空间的周期性，列出距离与波长关系的通项式．通过分析推理，深刻理解波动的本质，培养运用数学知识解决物理问题的能力．
练习册系列答案
相关题目
