题目内容

如图所示，在橄榄球比赛中，一个85kg的前锋队员以5m/s的速度跑动，想穿越防守队员到底线触地得分．就在他刚要到底线时，迎面撞上了对方两名均为65kg的队员，一个速度为2m/s，另一个速度为4m/s，然后他们就扭在了一起，则（　　）
分析：三个运动员所受合外力为零，动量守恒，根据动量守恒定律求出撞后共同速度，若此速度与前锋速度方向相同则可以得分．
解答：解：以前锋速度方向为正方向，设撞后共同速度为v，碰撞过程动量守恒，
根据动量守恒定律得：
m1v1-m2v2-m3v3=（m1+m2+m3）v
解得：v=
m1v1-m2v2-m3v3
m1m2+m3
=
85×5-65×2-65×4
85+65+65
m/s=0.16m/s，
所以他们碰撞后的共同速率为0.16m/s，方向与前锋方向相同，所以碰撞后他们动量的方向仍向前，能到达底线位置，所以AD错误BC正确．
故选BC
点评：本题主要考查了动量守恒定律得直接应用，知道撞后共同速度与前锋速度方向相同则可以得分，难度不大，属于基础题．
练习册系列答案
相关题目
选做题（请从A、B和C三小题中选定两小题作答，并在答题卡上把所选题目对应字母后的方框涂满涂黑．如都作答则按A、B两小题评分．）
A．（选修模块3-3）
（1）奥运祥云火炬的燃烧系统由燃气罐（内有液态丙烷）、稳压装置和燃烧器三部分组成，当稳压阀打开以后，燃气以气态形式从气罐里出来，经过稳压阀后进入燃烧室进行燃烧．则以下说法中正确的是
AC
AC
．
A．燃气由液态变为气态的过程中要对外做功
B．燃气由液态变为气态的过程中分子的分子势能减少
C．燃气在燃烧室燃烧的过程中分子的分子势能增加
D．燃气在燃烧后释放在周围环境中的能量很容易被回收再利用
（2）对于一定质量的理想气体，下列说法正确的是
BC
BC
．
A．如果保持气体的体积不变，温度升高，压强减小
B．如果保持气体的体积不变，温度升高，压强增大
C．如果保持气体的温度不变，体积越小，压强越大
D．如果保持气体的压强不变，温度越高，体积越小
（3）某运动员吸一口气，吸进400cm3的空气，据此估算他所吸进的空气分子的总数为
1×1022
1×1022
个．已知1mol气体处于标准状态时的体积是22.4L．（结果保留一位有效数字）
B．（选修模块3-4）
（1）在以下各种说法中，正确的是
ABC
ABC
．
A．四川汶川县发生8.0级强烈地震，地震波是机械波，其中既有横波也有纵波
B．相对论认为，真空中的光速在不同惯性参考系中都是相同的
C．如果测量到来自遥远星系上某些元素发出的光波波长比地球上这些元素静止时发光的波长长，这说明该星系正在远离我们而去
D．照相机镜头采用镀膜技术增加透射光，这是利用了光的衍射原理．
（2）一列横波在x轴上传播，图1甲为t=0时的波动图象，图1乙为介质中质点P的振动图象．该波的波长为
1
1
m，频率为
0.5
0.5
Hz，波速为
0.5
0.5
m/s，传播方向为
沿x轴向左
沿x轴向左
．
（3）如图2所示，一单色光束a，以入射角i=60°从平行玻璃砖上表面O点入射．已知平行玻璃砖厚度为d=10cm，玻璃对该单色光的折射率为n=
3
．则光束从上表面进入玻璃砖的折射角为
30°
30°
，光在玻璃砖中的传播的时间为
6.67×10-10s
6.67×10-10s
．
C．（选修模块3-5）
（1）在光电效应现象中，下列说法中正确的是
BC
BC
．
A．入射光的强度越大，光电子的最大初动能越大
B．光电子的最大初动能随照射光的频率增大而增大
C．对于任何一种金属都存在一个“最大波长”，入射光的波长必须小于此波长，才能产生光电效应
D．对于某种金属，只要入射光的强度足够大，就会发生光电效应
（2）铀（
 238
 92
U）经过α、β衰变形成稳定的铅（
 206
 82
U），问在这一变化过程中，共转变为质子的中子数是
6
6
个．
（3）在橄榄球比赛中，一个95kg的橄榄球前锋以5m/s的速度跑动，想穿越防守队员到底线触地得分．就在他刚要到底线时，迎面撞上了对方两名均为75kg的队员，一个速度为2m/s，另一个为4m/s，然后他们就扭在了一起．
①他们碰撞后的共同速率是
0.1m/s
0.1m/s
；
②在图3，右面方框中标出碰撞后他们动量的方向，并说明这名前锋能否得分：
能得分
能得分
．
选做题（请从A、B和C三小题中选定两小题作答，并在答题卡上把所选题目对应字母后的方框涂满涂黑．如都作答则按A、B两小题评分．）
A．（选修模块3-3）
（1）奥运祥云火炬的燃烧系统由燃气罐（内有液态丙烷）、稳压装置和燃烧器三部分组成，当稳压阀打开以后，燃气以气态形式从气罐里出来，经过稳压阀后进入燃烧室进行燃烧．则以下说法中正确的是______．
A．燃气由液态变为气态的过程中要对外做功
B．燃气由液态变为气态的过程中分子的分子势能减少
C．燃气在燃烧室燃烧的过程中分子的分子势能增加
D．燃气在燃烧后释放在周围环境中的能量很容易被回收再利用
（2）对于一定质量的理想气体，下列说法正确的是______．
A．如果保持气体的体积不变，温度升高，压强减小
B．如果保持气体的体积不变，温度升高，压强增大
C．如果保持气体的温度不变，体积越小，压强越大
D．如果保持气体的压强不变，温度越高，体积越小
（3）某运动员吸一口气，吸进400cm3的空气，据此估算他所吸进的空气分子的总数为______个．已知1mol气体处于标准状态时的体积是22.4L．（结果保留一位有效数字）
B．（选修模块3-4）
（1）在以下各种说法中，正确的是______．
A．四川汶川县发生8.0级强烈地震，地震波是机械波，其中既有横波也有纵波
B．相对论认为，真空中的光速在不同惯性参考系中都是相同的
C．如果测量到来自遥远星系上某些元素发出的光波波长比地球上这些元素静止时发光的波长长，这说明该星系正在远离我们而去
D．照相机镜头采用镀膜技术增加透射光，这是利用了光的衍射原理．
（2）一列横波在x轴上传播，图1甲为t=0时的波动图象，图1乙为介质中质点P的振动图象．该波的波长为______m，频率为______Hz，波速为______m/s，传播方向为______．
（3）如图2所示，一单色光束a，以入射角i=60°从平行玻璃砖上表面O点入射．已知平行玻璃砖厚度为d=10cm，玻璃对该单色光的折射率为n=
3
．则光束从上表面进入玻璃砖的折射角为______，光在玻璃砖中的传播的时间为______．
C．（选修模块3-5）
（1）在光电效应现象中，下列说法中正确的是______．
A．入射光的强度越大，光电子的最大初动能越大
B．光电子的最大初动能随照射光的频率增大而增大
C．对于任何一种金属都存在一个“最大波长”，入射光的波长必须小于此波长，才能产生光电效应
D．对于某种金属，只要入射光的强度足够大，就会发生光电效应
（2）铀（
 238
 92
U）经过α、β衰变形成稳定的铅（
 206
 82
U），问在这一变化过程中，共转变为质子的中子数是______个．
（3）在橄榄球比赛中，一个95kg的橄榄球前锋以5m/s的速度跑动，想穿越防守队员到底线触地得分．就在他刚要到底线时，迎面撞上了对方两名均为75kg的队员，一个速度为2m/s，另一个为4m/s，然后他们就扭在了一起．
①他们碰撞后的共同速率是______；
②在图3，右面方框中标出碰撞后他们动量的方向，并说明这名前锋能否得分：______．

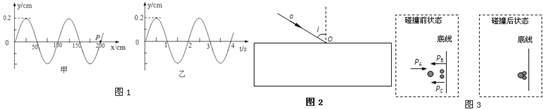
精英家教网
如图所示，在橄榄球比赛中，一个85kg的前锋队员以5m/s的速度跑动，想穿越防守队员到底线触地得分．就在他刚要到底线时，迎面撞上了对方两名均为65kg的队员，一个速度为2m/s，另一个速度为4m/s，然后他们就扭在了一起，则（ ）

A．他们碰撞后的共同速度是0.2 m/s
B．碰撞后他们动量的方向仍向前
C．这名前锋能得分
D．这名前锋不能得分
选做题（请从A、B和C三小题中选定两小题作答，并在答题卡上把所选题目对应字母后的方框涂满涂黑．如都作答则按A、B两小题评分．）
A．（选修模块3-3）
（1）奥运祥云火炬的燃烧系统由燃气罐（内有液态丙烷）、稳压装置和燃烧器三部分组成，当稳压阀打开以后，燃气以气态形式从气罐里出来，经过稳压阀后进入燃烧室进行燃烧．则以下说法中正确的是______．
A．燃气由液态变为气态的过程中要对外做功
B．燃气由液态变为气态的过程中分子的分子势能减少
C．燃气在燃烧室燃烧的过程中分子的分子势能增加
D．燃气在燃烧后释放在周围环境中的能量很容易被回收再利用
（2）对于一定质量的理想气体，下列说法正确的是______．
A．如果保持气体的体积不变，温度升高，压强减小
B．如果保持气体的体积不变，温度升高，压强增大
C．如果保持气体的温度不变，体积越小，压强越大
D．如果保持气体的压强不变，温度越高，体积越小
（3）某运动员吸一口气，吸进400cm3的空气，据此估算他所吸进的空气分子的总数为______个．已知1mol气体处于标准状态时的体积是22.4L．（结果保留一位有效数字）
B．（选修模块3-4）
（1）在以下各种说法中，正确的是______．
A．四川汶川县发生8.0级强烈地震，地震波是机械波，其中既有横波也有纵波
B．相对论认为，真空中的光速在不同惯性参考系中都是相同的
C．如果测量到来自遥远星系上某些元素发出的光波波长比地球上这些元素静止时发光的波长长，这说明该星系正在远离我们而去
D．照相机镜头采用镀膜技术增加透射光，这是利用了光的衍射原理．
（2）一列横波在x轴上传播，图1甲为t=0时的波动图象，图1乙为介质中质点P的振动图象．该波的波长为______m，频率为______Hz，波速为______m/s，传播方向为______．
（3）如图2所示，一单色光束a，以入射角i=60°从平行玻璃砖上表面O点入射．已知平行玻璃砖厚度为d=10cm，玻璃对该单色光的折射率为n=．则光束从上表面进入玻璃砖的折射角为______，光在玻璃砖中的传播的时间为______．
C．（选修模块3-5）
（1）在光电效应现象中，下列说法中正确的是______．
A．入射光的强度越大，光电子的最大初动能越大
B．光电子的最大初动能随照射光的频率增大而增大
C．对于任何一种金属都存在一个“最大波长”，入射光的波长必须小于此波长，才能产生光电效应
D．对于某种金属，只要入射光的强度足够大，就会发生光电效应
（2）铀（）经过α、β衰变形成稳定的铅（），问在这一变化过程中，共转变为质子的中子数是______个．
（3）在橄榄球比赛中，一个95kg的橄榄球前锋以5m/s的速度跑动，想穿越防守队员到底线触地得分．就在他刚要到底线时，迎面撞上了对方两名均为75kg的队员，一个速度为2m/s，另一个为4m/s，然后他们就扭在了一起．
①他们碰撞后的共同速率是______；
②在图3，右面方框中标出碰撞后他们动量的方向，并说明这名前锋能否得分：______．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网