Question

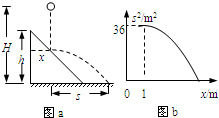如图a所示，倾角为45°、高为h的斜面固定在水平地面上，小球从高为H（2h＞H＞h）的某处自由下落，与斜面碰撞（无能量损失）后做平抛运动．若小球做平抛运动后能直接落到水平地面上，自由下落的起始点距斜面左端的水平距离x应满足的条件是

 

（用符号表示）；若测得x=1m时，小球平抛运动的水平射程s最大，且水平射程的平方s²与x关系如图b所示，则斜面的高h应为

 

m．

Answer 1

分析：小球与斜面碰撞后做平抛运动，当正好落在斜面底端时，x最小，根据平抛运动的基本公式结合几何关系、动能定理求出x的最小值，而x的最大值即为h，从而求出x的范围；由图可知，当x=1m时，s最大，且s²=36m²，所以s=6m，根据平抛运动的基本公式及动能定理求出s²的表达式，根据数学知识求出满足什么条件时，s最大，从而求解h．

解答：解：小球与斜面碰撞后做平抛运动，当正好落在斜面底端时，根据几何关系可知，
水平位移x₁=h-x
竖直位移y=h-x
根据平抛运动竖直方向做自由落体运动得：
t=

2(h-x) g

所以平抛运动的初速度为v0=

h-x

t

=

h-x

2(h-x) g

小球从释放到与斜面碰撞的过程中，根据动能定理得：
mg（H+x-h）=

1

2

mv02
解得：x=h-

4

5

H
当小球正好在斜面底端释放时，x最大，则x_max=h
所以若小球做平抛运动后能直接落到水平地面上，自由下落的起始点距斜面左端的水平距离x应满足的条件是h＞x＞h-

4

5

H；
由图可知，当x=1m时，s²=36m²，所以s=6m
则水平方向：s=vt，
竖直方向：h-x=

1

2

gt²，
根据动能定理得：
2g（H-h+x）=v²，
联立解得
s²=4（H-h+x）（h-x）=-4[（h-x）²-H（h-x）+

1

4

H²]+H²=-4[（h-x）-

H

2

]²+H²．
当（h-x）-

H

2

=0时，s²取最大值，s最大值为6m，对应的H=6m，斜面的高h=x+

H

2

=4m
故答案为：h＞x＞h-

4

5

H；4

点评：本题主要考查了平抛运动基本公式、动能定理的直接应用，要求同学们能结合数学知识求解s的最大值，难度适中．