Question

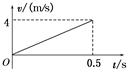
质量为0.1 kg的弹性球从空中某高度由静止开始下落，该下落过程对应的v－t图象如图所示。球与水平地面相碰后离开地面时的速度大小为碰撞前的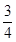。设球受到的空气阻力大小恒为f，取g＝10 m/s²，求：   

   

(1)弹性球受到的空气阻力f的大小；

(2)弹性球第一次碰撞后反弹的高度h。

 

Answer 1

【答案】

（1）0.2 N（2）h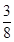＝m

【解析】

试题分析：(1)设弹性球第一次下落过程中的加速度大小为a₁，由图知

a₁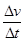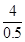＝＝m/s²＝8 m/s²

根据牛顿第二定律，得

mg－f＝ma₁       f＝m(g－a₁)＝0.2 N

(2)由题图知弹性球第一次到达地面时的速度大小为v₁＝4 m/s，设球第一次离开地面时的速度大小为v₂，则v₂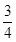＝v₁＝3 m/s

第一次离开地面后，设上升过程中球的加速度大小为a₂，则mg＋f＝ma₂，a₂＝12 m/s²

于是，有0－v₂²＝－2a₂h  解得h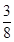＝m。

考点：牛顿第二定律；匀变速直线运动的图像．

点评：牛顿运动定律和运动学公式结合是处理动力学问题常用的方法．速度图象要抓住两个意义：斜率表示加速度，“面积”表示位移．