题目内容
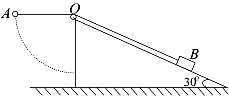
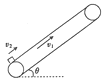
【题目】如图所示，一传送带与水平面的夹角θ= 300，且以v1=2 m/s的速度沿顺时针方向传动。一小物块以v2=4 m/s的速度从底端滑上传送带，最终又从传送带的底端滑出。已知物块与传送带间的动摩擦因数
，传送带足够长，取重力加速度g=10 m／s2。求：
(1)小物块沿传送带向上滑行的时间t；
(2)小物块离开传送带时的速度大小v。
【答案】(1) 
(2) 
【解析】（1）由题可知，小物块在开始时受到传送带的滑动摩擦力沿传送带向下，设其做匀减速运动的加速度大小为
，有： 
，解得
其速度减小到
，所用的时间为
之后，小物块受到传送带的滑动摩擦力沿传送带向上，设其加速度大小为
有： 
，解得
小物块减速到0所用的时间为： 
又
（2）小物块沿传送带向上滑行的最大距离为
解得
又由于物块沿传送带下滑时，受到的滑动摩擦力沿传送带向上，其加速度大小仍为
，有： 
，解得
练习册系列答案
阅读快车系列答案
相关题目
