��Ŀ����
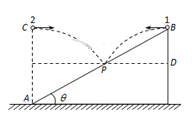
����Ŀ����ͼ��ʾ������а뾶ΪR��Բ�������ڴ�����ǿ�ų����ų�����ֱֽ������ڴų������һ��ƽ�н�����M��N��������Ϊ2R���峤ΪL���������������Բ��O��ͬһˮƽ���ϡ�����Q��������Դ�����������ٶ�v0������������߷�������Ϊq������Ϊm�Ĵ���������ӣ�����������������MN���岻�ӵ�ѹʱ�����Ӿ��ų�ƫת��ǡ�ô�Բ�δų�Բ�����Ϸ���P���뿪������MN��������ͼ��ʾ�Ľ����ѹ�������ѹ������Ϊ![]() ��t=0ʱ�����������ǡ�ý�����N���Ҳ�ˮƽ�������
��t=0ʱ�����������ǡ�ý�����N���Ҳ�ˮƽ�������

��1����ǿ�ų��ĴŸ�ǿ��B�Ĵ�С��
��2�������ѹU0��ֵ��
��3���ڵ�һ�����ڣ���ʱ����糡������ǡ�þ����ų���Բ�ġ�
���𰸡���1��![]() ��2��
��2��![]() ��3��
��3��![]()
��������
���ݼ��ι�ϵ��������ڴų����˶��Ĺ���뾶����ϰ뾶��ʽ�����ǿ�ų��ĴŸ�Ӧǿ�ȴ�С������ƫתλ�ƵĴ�С�����ţ�ٵڶ����ɺ��˶�ѧ��ʽ��������ѹU0��ֵ�����������ڵ糡�е��˶�ʱ��ΪT�������ӽ���ų�ʱ���ٶȷ���ʼ����ˮƽ����СΪ![]() �������ڵ糡�е�һ�μ�������һ�η���������ɼ���֪ʶ�ý���糡�����ӵ�ʱ�䣻
�������ڵ糡�е�һ�μ�������һ�η���������ɼ���֪ʶ�ý���糡�����ӵ�ʱ�䣻
������(1)�ɼ���֪ʶ�ã�Բ���˶��İ뾶Ϊ��![]()
��ţ�ٵڶ����ɵã�![]()
��ã� ![]()
(2)������ƽ�а����ֱ������ٶ�ʱ����ţ�ٵڶ����ɵã� ![]()
��ֱ�������λ��Ϊ��![]()
����ֱ�����˶��ĶԳ���֪��![]()
�����������![]()
(3)�����Ӵ�![]() ʱ�̽���糡ǡ���ܹ�Բ�ģ����������ڵ糡�е��˶�ʱ��ΪT�������ӽ���ų�ʱ���ٶȷ���ʼ����ˮƽ����СΪ
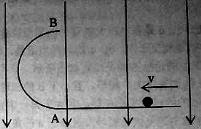
ʱ�̽���糡ǡ���ܹ�Բ�ģ����������ڵ糡�е��˶�ʱ��ΪT�������ӽ���ų�ʱ���ٶȷ���ʼ����ˮƽ����СΪ![]() �������˶��Ĺ켣��ͼ��ʾ���ɼ���֪ʶ����AO1OΪ�ȱ���������
�������˶��Ĺ켣��ͼ��ʾ���ɼ���֪ʶ����AO1OΪ�ȱ���������
�����ڵ糡�е�һ�μ���λ���� ![]()
��һ�η�����ٵ�λ����![]()
���������![]()
���������![]()


 ����ѵ�����⿼ϵ�д�
����ѵ�����⿼ϵ�д�