题目内容
如图所示,用一连接体一端与一小球相连,绕过O点的水平轴在竖直平面内做圆周运动,设轨道半径为r,图中P、Q两点分别表示小球轨道的最高点和最低点,则以下说法正确的是( )
A.若连接体是轻质细绳时,小球到达P点的速度可以为零
B.若连接体是轻质细杆时,小球到达P点的速度可以为零
C.若连接体是轻质细绳时,小球在P点受到细绳的拉力不可能为零
D.若连接体是轻质细杆时,小球在P点受到细杆的作用力为拉力,在Q点受到细杆的作用力为推力

【解析】选B。若连接体是轻质细绳,小球在最高点的最小速度为![]() ,此时细绳拉力为零,选项A、C错误;若连接体是轻质细杆,小球刚好到达P点的速度为零,选项B正确;如果小球在最高点P的速度为
,此时细绳拉力为零,选项A、C错误;若连接体是轻质细杆,小球刚好到达P点的速度为零,选项B正确;如果小球在最高点P的速度为![]() ,细杆拉力为零,如果v>
,细杆拉力为零,如果v>![]() ,细杆的作用力为拉力,如果v<
,细杆的作用力为拉力,如果v<![]() ,细杆的作用力为推力,小球在最低点Q时受到细杆的拉力作用,选项D错误。
,细杆的作用力为推力,小球在最低点Q时受到细杆的拉力作用,选项D错误。
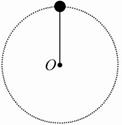
【变式备选】小明同学在学习中勤于思考,并且善于动手,在学习了圆周运动知识后,他自制了一个玩具,如图所示,用长为r的细杆粘住一个质量为m的小球,使之绕另一端O在竖直平面内做圆周运动,小球运动到最高点时的速度v=![]() ,在这点时( )
,在这点时( )
A.小球对细杆的拉力是![]()
B.小球对细杆的压力是![]()
C.小球对细杆的拉力是![]()
D.小球对细杆的压力是mg
【解析】选B。解法一:在最高点时,若细杆对小球没有弹力作用,则有mg=![]() ,得v0=
,得v0=![]() 。由于v=
。由于v=![]() <v0,所以细杆对小球有竖直向上的弹力作用,根据牛顿第二定律和向心力公式有mg-FN=
<v0,所以细杆对小球有竖直向上的弹力作用,根据牛顿第二定律和向心力公式有mg-FN=![]() ,得FN=
,得FN=![]() 。由牛顿第三定律知,小球对细杆的压力FN′=FN=
。由牛顿第三定律知,小球对细杆的压力FN′=FN=![]() 。故选B。
。故选B。
解法二:假设细杆对小球有竖直向下的拉力,根据牛顿第二定律和向心力公式有mg+FN=![]() ,得
,得![]() ,负号说明细杆对小球有竖直向上的支持力。由牛顿第三定律知,小球对细杆的压力FN′=FN=
,负号说明细杆对小球有竖直向上的支持力。由牛顿第三定律知,小球对细杆的压力FN′=FN=![]() 。故选B。
。故选B。

如图所示,用一连接体一端与一小球相连,绕过O点的水平轴在竖直平面内做圆周运动,设轨道半径为r,图中P、Q两点分别表示小球轨道的最高点和最低点,则以下说法正确的是
| A.若连接体是轻质细绳时,小球到达P点的速度可以为零 |
| B.若连接体是轻质细杆时,小球到达P点的速度一定不能为零 |
| C.若连接体是轻质细绳时,小球在P点受到细绳的拉力一定为零 |
| D.若连接体是轻质细杆时,小球在Q点受到细杆的拉力一定竖直向上 |
 (2006?济南模拟)如图所示,用一连接体一端与一小球相连,绕过O点的水平轴在竖直平面内做圆周运动,设轨道半径为r,图中P、Q两点分别表示小球轨道的最高点和最低点,则以下说法正确的是( )
(2006?济南模拟)如图所示,用一连接体一端与一小球相连,绕过O点的水平轴在竖直平面内做圆周运动,设轨道半径为r,图中P、Q两点分别表示小球轨道的最高点和最低点,则以下说法正确的是( ) 如图所示,用一连接体一端与一小球相连,绕过O点的水平轴在竖直平面内做圆周运动,设轨道半径为r,图中P、Q两点分别表示小球轨道的最高点和最低点,则以下说法正确的是
如图所示,用一连接体一端与一小球相连,绕过O点的水平轴在竖直平面内做圆周运动,设轨道半径为r,图中P、Q两点分别表示小球轨道的最高点和最低点,则以下说法正确的是