Question

如图所示，套在很长的绝缘直棒上的带正电的小球，其质量为m，带电荷量为q，小球可在棒上滑动，现将此棒竖直放在互相垂直且沿水平方向的匀强电场和匀强磁场中，电场强度是E，磁感应强度是B，小球与棒的动摩擦因数为μ，求小球由静止沿棒下落的最大加速度和最大速度(设小球电荷量不变)．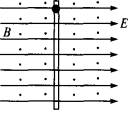

 

Answer 1

答案：
解析：

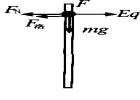
解析：球在下滑过程中将受到重力、电场力、杆对球的弹力、杆对球的滑动摩擦力和洛伦兹力，其中重力向下，滑动摩擦力向上，电场力向右．下滑之前，球运动速度为零，洛伦兹力为零，杆对球的弹力向左，且弹力等于电场力(注意此时并不是弹力最小、加速度最大时刻)．当球开始下滑后，水平方向除受电场力、弹力外，还受到向左的洛伦兹力，此时，弹力等于电场力和洛伦兹力之差．由于刚开始下滑，球速度较小，洛伦兹力小于电场力．随着下滑速度的变大，洛伦兹力变大，导致弹力变小，球下滑的加速度将变大．当球速度大到使洛伦兹力等于电场力时，弹力为零，球受到的摩擦力为零．此时，球下滑的加速度达到最大值，且刚好等于重力加速度g．随着球的速度继续变大，洛伦兹力大于电场力，弹力等于洛伦兹力和电场力之差．随着球的速度增加，弹力变大，摩擦力变大，球下滑的加速度变小，当摩擦力大到等于重力时，球将匀速下滑，此时球的速度即为最大速度． 小球下滑开始阶段的受力情况如图所示，根据牛顿第二定律有： 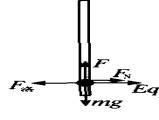mg－μFN＝ma 且FN＝Eq－F洛＝Eq－qvB 当v大到F洛=Eq， 即v1＝Eq/qB时， 摩擦力F＝0，则： amax＝g 当v＞v1时，小球受力情况如图所示： 由牛顿第二定律有：mg－μFN＝ma 且FN＝F洛－Eq F洛＝qvB 当v大到F＝mg时，a＝0，此时v达到最大 值，即：mg＝μ(qvB－Eq) 得vmax＝ 答案：g 说明：分析该题中球运动状态的变化：v↑→F洛↑→FN 大小及方向变化→F先↓后↑→a先↑后↓．小球的运动可 划分为三个阶段，要对各阶段认真进行受力分析，明确各量如 何变化，找出极值条件．本题中F洛＝qE，即FN＝0、F＝0时， a最大；F合＝0，即F＝mg时，v最大．

提示：