题目内容
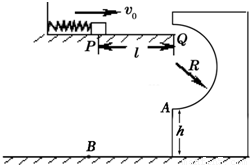
如图所示,水平轨道上轻弹簧左端固定,弹簧处于自然状态时,其右端位于P点.现用一质量m=0.1kg的小物块 (可视为质点)将弹簧压缩后释放,物块经过P点时的速度v=18m/s,经过水平轨道右端Q点后恰好沿半圆轨道的切线进入竖直固定的光滑圆轨道,最后物块经轨道最低点A抛出后落到B点,若物块与水平轨道间的动摩擦因数μ=0.15,R=lm,A到B的竖直高度h=1.25m,取g=10m/s2.(1)求物块到达Q点时的速度大小(保留根号);
(2)判断物块经过Q点后能否沿圆周轨道运动;
(3)求物块水平抛出的位移大小.
【答案】分析:首先要了解问题的运动过程,运用动能定理研究P到Q可求解Q的速度大小,运用机械能守恒定律或动能定理研究Q到A可求解A的速度大小,再运用平抛运动的知识求解水平位移.
解答:解:(1)设物块到达Q点时的速度为v,由动能定理得:
-μmg l= mv2-
mv2- mv2;
mv2;
代入数据解得v=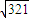 m/s.
m/s.
(2)设物块刚离开Q点时,圆轨道对物块的压力为FN,
根据牛顿定律有FN+mg=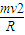 ;
;
则FN=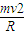 -mg=31.1N>0;
-mg=31.1N>0;
故物块能沿圆周轨道运动.
(3)设物块到达半圆轨道最低点A时的速度为v1,
由机械能守恒得: mv2+mg?2R=
mv2+mg?2R= mv12 ;
mv12 ;
解得v1=19 m/s;
由 h= gt2,s=vt;
gt2,s=vt;
得s=v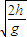 ;
;
代入数据,得s=9.5m.
答:(1)物块到达Q点时的速度大小是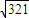 m/s;
m/s;
(2)物块能沿圆周轨道运动;
(3)物块水平抛出的位移大小是9.5m.
点评:该题考查了多个知识点的应用,动能定理应用注意研究过程的选取,要通过正确的受力分析找到向心力的来源,对于Q到A的过程可以运用机械能守恒定律或动能定理研究.
解答:解:(1)设物块到达Q点时的速度为v,由动能定理得:
-μmg l=
 mv2-
mv2- mv2;
mv2; 代入数据解得v=
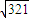 m/s.
m/s. (2)设物块刚离开Q点时,圆轨道对物块的压力为FN,
根据牛顿定律有FN+mg=
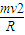 ;
; 则FN=
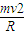 -mg=31.1N>0;
-mg=31.1N>0;故物块能沿圆周轨道运动.
(3)设物块到达半圆轨道最低点A时的速度为v1,
由机械能守恒得:
 mv2+mg?2R=
mv2+mg?2R= mv12 ;
mv12 ;解得v1=19 m/s;
由 h=
 gt2,s=vt;
gt2,s=vt; 得s=v
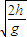 ;
; 代入数据,得s=9.5m.
答:(1)物块到达Q点时的速度大小是
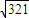 m/s;
m/s;(2)物块能沿圆周轨道运动;
(3)物块水平抛出的位移大小是9.5m.
点评:该题考查了多个知识点的应用,动能定理应用注意研究过程的选取,要通过正确的受力分析找到向心力的来源,对于Q到A的过程可以运用机械能守恒定律或动能定理研究.

练习册系列答案
相关题目
 如图所示,水平轨道上轻弹簧左端固定,弹簧处于自然状态时,其右端位于P点,现用一质量m=0.1kg的小物块(可视为质点)将弹簧压缩后释放,物块经过P点时的速度v0=6m/s,经过水平轨道右端Q点后恰好沿半圆光滑轨道的切线进入竖直固定的圆轨道,最后物块经轨道最低点A抛出后落到B点,若物块与水平轨道间的动摩擦因数μ=0.15,s=4m,R=1m,A到B的竖直高度h=1.25m,取g=10m/s2.
如图所示,水平轨道上轻弹簧左端固定,弹簧处于自然状态时,其右端位于P点,现用一质量m=0.1kg的小物块(可视为质点)将弹簧压缩后释放,物块经过P点时的速度v0=6m/s,经过水平轨道右端Q点后恰好沿半圆光滑轨道的切线进入竖直固定的圆轨道,最后物块经轨道最低点A抛出后落到B点,若物块与水平轨道间的动摩擦因数μ=0.15,s=4m,R=1m,A到B的竖直高度h=1.25m,取g=10m/s2. (2012?东至县模拟)如图所示,水平轨道上,轻弹簧左端固定,自然状态时右端位于P点.现用一质量m=0.1kg的小物块(视为质点)将弹簧压缩后释放,物块经过P点时的速度v0=18m/s,经过水平轨道右端Q点后恰好沿半圆轨道的切线进入竖直固定的圆轨道,最后滑上质量M=0.9kg的长木板(木板足够长,物块滑上去不会从木板上掉下来).已知PQ间的距离l=1m,竖直半圆轨道光滑且半径R=1m,物块与水平轨道间的动摩擦因数?1=0.15,与木板间的动摩擦因数?2=0.2,木板与水平地面间的动摩擦因数?3=0.01,取g=10m/s2.
(2012?东至县模拟)如图所示,水平轨道上,轻弹簧左端固定,自然状态时右端位于P点.现用一质量m=0.1kg的小物块(视为质点)将弹簧压缩后释放,物块经过P点时的速度v0=18m/s,经过水平轨道右端Q点后恰好沿半圆轨道的切线进入竖直固定的圆轨道,最后滑上质量M=0.9kg的长木板(木板足够长,物块滑上去不会从木板上掉下来).已知PQ间的距离l=1m,竖直半圆轨道光滑且半径R=1m,物块与水平轨道间的动摩擦因数?1=0.15,与木板间的动摩擦因数?2=0.2,木板与水平地面间的动摩擦因数?3=0.01,取g=10m/s2. (2011?烟台模拟)如图所示,水平轨道上轻弹簧左端固定,弹簧处于自然状态时,其右端位于P点.现用一质量m=0.1kg的小物块 (可视为质点)将弹簧压缩后释放,物块经过P点时的速度v0=18m/s,经过水平轨道右端Q点后恰好沿半圆轨道的切线进入竖直固定的光滑圆轨道,最后物块经轨道最低点A抛出后落到B点,若物块与水平轨道间的动摩擦因数μ=0.15,R=lm,A到B的竖直高度h=1.25m,取g=10m/s2.
(2011?烟台模拟)如图所示,水平轨道上轻弹簧左端固定,弹簧处于自然状态时,其右端位于P点.现用一质量m=0.1kg的小物块 (可视为质点)将弹簧压缩后释放,物块经过P点时的速度v0=18m/s,经过水平轨道右端Q点后恰好沿半圆轨道的切线进入竖直固定的光滑圆轨道,最后物块经轨道最低点A抛出后落到B点,若物块与水平轨道间的动摩擦因数μ=0.15,R=lm,A到B的竖直高度h=1.25m,取g=10m/s2.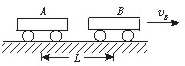 如图所示,水平轨道上停放着一辆质量为5.0×102 kg的小车A,在A的右方L=8.0m处,另一辆小车B正以速度vB=4.0m/s的速度向右做匀速直线运动远离A车,为使A车能经过t=10.0s时间追上B车,立即给A车适当施加向右的水平推力使小车做匀变速直线运动,设小车A受到水平轨道的阻力是车重的0.1倍,试问:在此追及过程中,推力至少需要做多少功?取g=10m/s2)
如图所示,水平轨道上停放着一辆质量为5.0×102 kg的小车A,在A的右方L=8.0m处,另一辆小车B正以速度vB=4.0m/s的速度向右做匀速直线运动远离A车,为使A车能经过t=10.0s时间追上B车,立即给A车适当施加向右的水平推力使小车做匀变速直线运动,设小车A受到水平轨道的阻力是车重的0.1倍,试问:在此追及过程中,推力至少需要做多少功?取g=10m/s2)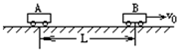 如图所示,水平轨道上停放着一辆质量为5.0×102kg的小车A,在A的右方L=8.0m处,另一辆小车B正以速度v0=4.0m/s向右做匀速运动远离A车,为使A车经过t=10.0s时间追上B上,立即给A适当施加向右水平推力使小车做匀变速直线运动,设小车A受到水平轨道的阻力是车重的0.1倍,试问:在此追及过程中,推力至少需要做
如图所示,水平轨道上停放着一辆质量为5.0×102kg的小车A,在A的右方L=8.0m处,另一辆小车B正以速度v0=4.0m/s向右做匀速运动远离A车,为使A车经过t=10.0s时间追上B上,立即给A适当施加向右水平推力使小车做匀变速直线运动,设小车A受到水平轨道的阻力是车重的0.1倍,试问:在此追及过程中,推力至少需要做