题目内容
 (2013?红桥区一模)如图所示,相距为d的L1和L2两条平行虚线是上下两个匀强磁场的边界,L1上方和L2下方都是垂直纸面向里的磁感应强度为B的匀强磁场,M、N两点都在L2上,M点有一放射源其放射性元素衰变前原子核的质量为m,它释放出一个质量为m1,带电量为-q的粒子后,产生的新原子核质量为m2,释放出的粒子以初速度v与L2成30°角斜向上射入,经过一段时间恰好斜向上通过N点(不计重力),求:
(2013?红桥区一模)如图所示,相距为d的L1和L2两条平行虚线是上下两个匀强磁场的边界,L1上方和L2下方都是垂直纸面向里的磁感应强度为B的匀强磁场,M、N两点都在L2上,M点有一放射源其放射性元素衰变前原子核的质量为m,它释放出一个质量为m1,带电量为-q的粒子后,产生的新原子核质量为m2,释放出的粒子以初速度v与L2成30°角斜向上射入,经过一段时间恰好斜向上通过N点(不计重力),求:(1)该原子核发生衰变的过程中释放的核能;
(2)说明粒子过N点时的速度大小和方向,并求从M到N的时间及路程.
分析:(1)根据爱因斯坦的质能联系方程即可求解;
(2)由洛伦兹力提供向心力,列出半径与周期公式;再由几何知识结合运动轨迹可确定速度大小与方向,同时算出总时间与总路程.
(2)由洛伦兹力提供向心力,列出半径与周期公式;再由几何知识结合运动轨迹可确定速度大小与方向,同时算出总时间与总路程.
解答:解:(1)由爱因斯坦的质能联系方程可知△E=△mc2=(m-m1-m2)c2
(2)由洛仑兹力提供向心力:qvB=
可知R=
; T=

由几何知识及匀速圆周运动的对称性可知N点的速度大小仍为v,方向斜向上300
运动总时间为:t总=
+
总路程为:S总=4d+
答:(1)该原子核发生衰变的过程中释放的核能(m-m1-m2)c2;
(2)粒子过N点时的速度大小仍为v,方向斜向上300,且从M到N的时间为
+
及路程为4d+
.
(2)由洛仑兹力提供向心力:qvB=
| mv2 |
| R |
可知R=
| mv |
| Bq |
| 2πm |
| qB |

由几何知识及匀速圆周运动的对称性可知N点的速度大小仍为v,方向斜向上300
运动总时间为:t总=
| 4d |
| v |
| 2πm |
| qB |
总路程为:S总=4d+
| 2πmv |
| qB |
答:(1)该原子核发生衰变的过程中释放的核能(m-m1-m2)c2;
(2)粒子过N点时的速度大小仍为v,方向斜向上300,且从M到N的时间为
| 4d |
| v |
| 2πm |
| qB |
| 2πmv |
| qB |
点评:涉及爱因斯坦的质能方程、牛顿第二定律、运动学公式等规律,并结合几何知识来综合解题.同时注意洛伦兹力的方向性.

练习册系列答案
 中考利剑中考试卷汇编系列答案
中考利剑中考试卷汇编系列答案 教育世家状元卷系列答案
教育世家状元卷系列答案 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案 单元加期末复习先锋大考卷系列答案
单元加期末复习先锋大考卷系列答案
相关题目
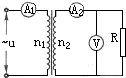 (2013?红桥区一模)如图所示,一理想变压器原线圈匝数n1=1100匝,副线圈匝数n2=220匝,交流电源的电压U=220
(2013?红桥区一模)如图所示,一理想变压器原线圈匝数n1=1100匝,副线圈匝数n2=220匝,交流电源的电压U=220 (2013?红桥区一模)两物体A和B,质量分别为m1和m2,互相接触放在光滑水平面上,如图所示.对物体A施以水平的推力F,则物体A对物体B的作用力等于( )
(2013?红桥区一模)两物体A和B,质量分别为m1和m2,互相接触放在光滑水平面上,如图所示.对物体A施以水平的推力F,则物体A对物体B的作用力等于( ) (2013?红桥区一模)用a、b两束单色光分别照射同一双缝干涉装置,在距双缝恒定距离的屏上得到如图示的干涉图样,其中甲图是a光照射时形成的,乙图是b光照射时形成的.则关于a、b两束单色光,下述正确的是( )
(2013?红桥区一模)用a、b两束单色光分别照射同一双缝干涉装置,在距双缝恒定距离的屏上得到如图示的干涉图样,其中甲图是a光照射时形成的,乙图是b光照射时形成的.则关于a、b两束单色光,下述正确的是( ) (2013?红桥区一模)如图所示的电路中,电流表Al与A2为相同的毫安表(内阻不能忽略),当电路两端接入某一恒定电压的电源时,Al的示数为5mA,A2的示数为3mA.现将A2改接在R2所在的支路上,如图中虚线所示,再接到原来的恒定电源上,图中的电表均不会烧坏,那么下列说法中正确的是( )
(2013?红桥区一模)如图所示的电路中,电流表Al与A2为相同的毫安表(内阻不能忽略),当电路两端接入某一恒定电压的电源时,Al的示数为5mA,A2的示数为3mA.现将A2改接在R2所在的支路上,如图中虚线所示,再接到原来的恒定电源上,图中的电表均不会烧坏,那么下列说法中正确的是( )