题目内容
天花板下悬挂轻质光滑小圆环P，P可绕着过悬挂点的竖直轴无摩擦地旋转，长为L的轻绳穿过P，两端分别连接质量m1和m2的小球，设两球同时作如图所示的圆锥摆运动，且在任一时刻两球和绳均在同一竖直平面内，试求两小球各自到P点的距离l1和l2．
【答案】分析：光滑的小圆环P相当于定滑轮，因此连接小球的绳子上拉力大小相等，分别以两球为研究对象，受力分析列向心力方程即可正确解答，注意两球的角速度相等．
解答：解：连接两球的绳子拉力相等，两球的角速度相等，
设绳子上拉力为T，对小球m1和m2分别有：
对m1：r1=l1sinφ1 ①
②
对m2：r2=l2sinφ2 ③
④
联立①②③④得：m1l1=m2l2，由于l1+l2=L
所以：
，
．
故两小球各自到P点的距离为：
，
．
点评：对于圆周运动问题注意做题思路：找圆心，定半径，受力分析，列方程，尤其注意列出向心力公式方程，进行求解．
解答：解：连接两球的绳子拉力相等，两球的角速度相等，
设绳子上拉力为T，对小球m1和m2分别有：
对m1：r1=l1sinφ1 ①
②对m2：r2=l2sinφ2 ③
④联立①②③④得：m1l1=m2l2，由于l1+l2=L
所以：
，．故两小球各自到P点的距离为：
，．点评：对于圆周运动问题注意做题思路：找圆心，定半径，受力分析，列方程，尤其注意列出向心力公式方程，进行求解．
练习册系列答案
相关题目
天花板下悬挂轻质光滑小圆环P，P可绕着过悬挂点的竖直轴无摩擦地旋转，长为L的轻绳穿过P，两端分别连接质量m1和m2的小球，设两球同时作如图所示的圆锥摆运动，且在任一时刻两球和绳均在同一竖直平面内，试求两小球各自到P点的距离l1和l2．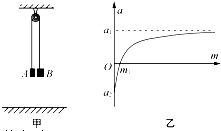
如图甲所示，水平天花板下悬挂一光滑的轻质的定滑轮，跨过定滑轮的质量不计的绳（绳承受拉力足够大）两端分别连接物块A和B，A的质量为m0，B的质量m是可以变化的，当B的质量改变时，可以得到A加速度变化图线如图乙所示，不计空气阻力和所有的摩擦，A加速度向上为正．
天花板下悬挂轻质光滑小圆环P，P可绕着过悬挂点的竖直轴无摩擦地旋转，长为L的轻绳穿过P，两端分别连接质量m1和m2的小球，设两球同时作如图所示的圆锥摆运动，且在任一时刻两球和绳均在同一竖直平面内，试求两小球各自到P点的距离l1和l2．