题目内容
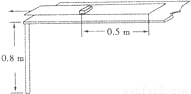
如图所示，静止放在长直水平桌面上的纸带．其上有一小铁块，它与纸带右端的距离为0.5m，铁块与纸带间、纸带与桌面间动摩擦因数均为μ=0.1．现用力F水平向左将纸带从铁块下抽出，当纸带全部抽出时铁块恰好到达桌面边缘，铁块抛出后落地点离抛出点的水平距离为x=0.8m．已知g=10m/s2，桌面高度为H=0.8m，不计铁块大小，铁块不滚动．求：（1）铁块落地时的速度大小．
（2）纸带从铁块下抽出所用的时间及开始时铁块距左侧桌边的距离．
【答案】分析：（1）铁块离开桌面后做平抛运动，根据分位移公式列式求解得到初速度；
（2）对铁块受力分析，根据牛顿第二定律求出加速度，然后根据位移公式求得铁块的初位置与桌边的距离和铁块直线加速的时间．
解答：解：（1）设铁块抛出时的初速度为v，由平抛运动规律，有
水平方向：x=vt
竖直方向：H=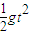
解得
v=2m/s
由机械能守恒定律，可得：
mgH+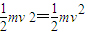
解得
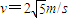
故纸带从铁铁块落地时的速度大小为2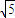
m/s．
（2）纸带从铁块下抽出所用的时间与铁块向左运动到桌边的时间相等．
开始时距离桌面左端的距离就等于铁块在桌面上向左运动的位移．
铁块向左运动过程中，a=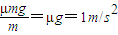
铁块从静止开始向左运动的位移为L，由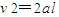
，得L=2m．
由公式v=at，得t=2s
故纸带从铁块下抽出所用的时间为2s，开始时铁块距左侧桌边的距离2m．
点评：本题关键是先分析清楚物体的运动情况，然后运用平抛运动的分位移公式、牛顿运动定律和运动学公式联立列式求解．
（2）对铁块受力分析，根据牛顿第二定律求出加速度，然后根据位移公式求得铁块的初位置与桌边的距离和铁块直线加速的时间．
解答：解：（1）设铁块抛出时的初速度为v，由平抛运动规律，有
水平方向：x=vt
竖直方向：H=
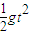
解得
v=2m/s
由机械能守恒定律，可得：
mgH+
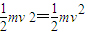
解得
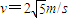
故纸带从铁铁块落地时的速度大小为2
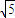m/s．（2）纸带从铁块下抽出所用的时间与铁块向左运动到桌边的时间相等．
开始时距离桌面左端的距离就等于铁块在桌面上向左运动的位移．
铁块向左运动过程中，a=
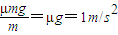
铁块从静止开始向左运动的位移为L，由
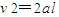，得L=2m．由公式v=at，得t=2s
故纸带从铁块下抽出所用的时间为2s，开始时铁块距左侧桌边的距离2m．
点评：本题关键是先分析清楚物体的运动情况，然后运用平抛运动的分位移公式、牛顿运动定律和运动学公式联立列式求解．
练习册系列答案
初中学业考试导与练系列答案
相关题目
如图所示，一根长L=0.2m的金属棒放在倾角为θ=37°的光滑斜面上，并通以I=5A电流，方向如图所示，整个装置放在磁感应强度为B=0.6T，竖直向上的匀强磁场中，金属棒恰能静止在斜面上，则该棒的重力为多少？（sin37°=0.6）
如图所示，一足够长的木板B放在水平地面上，木块A放在B的水平表面上，A的左端连有轻质弹簧，弹簧左端固定在竖直墙壁上，用力F向右拉动=木板B，使B以速度v做匀速运动，A相对地面静止时，弹簧的弹力为F1．已知木块与木板之间、木板和地面之=间的动摩擦因数相同，A终在B上，则以下说法中正确的是（ ）
如图所示，静止放在长直水平桌面上的纸带．其上有一小铁块，它与纸带右端的距离为0.5m，铁块与纸带间、纸带与桌面间动摩擦因数均为μ=0.1．现用力F水平向左将纸带从铁块下抽出，当纸带全部抽出时铁块恰好到达桌面边缘，铁块抛出后落地点离抛出点的水平距离为x=0.8m．已知g=10m/s2，桌面高度为H=0.8m，不计铁块大小，铁块不滚动．求：
如图所示，光滑的长平行金属导轨宽度d=50cm，导轨所在的平面与水平面夹角θ=37°，导轨上端电阻R=0.8Ω，其他电阻不计，导轨放在垂直于斜面向上的匀强磁场中，磁感应强度B=0.4T．金属棒ab从上端由静止开始下滑，金属棒ab的质量m=0.1kg．（sin37°=0.6，g=10m/s2）求：