题目内容
一粗细均匀的J型玻璃管竖直放置,短臂端封闭,长臂端(足够长)开口向上,短臂内封有一定质量的理想气体.初始状态时管内各段长度如图(a)所标,密闭气体的温度为27℃.大气压强为75cmHg,求:(1)若沿长臂的管壁缓慢加入5cm的水银柱并与下方的水银合为一体,为使密闭气体保持原来的长度,应使气体的温度变为多少?
(2)在第(1)小题的情况下,再使玻璃管沿绕过O点的水平轴在竖直平面内逆时针转过180°,稳定后密闭气体的长度变为多大?
(3)在图(b)的p-T坐标系中画出以上两个过程中密闭气体的状态变化过程.
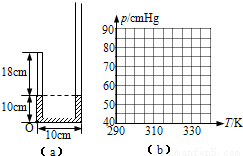
【答案】分析:(1)根据玻璃管两边的液面差,求出两个状态下气体的压强,气体做等容变化,根据气态方程即可求出后来气体的温度.
(2)通过假设的方法判断当玻璃管沿绕过O点的水平轴在竖直平面内逆时针转过180°时短臂内是否有水银,然后根据等温变化求解.
(3)根据两个过程中气体状态变化的特点可以画出该图象.
解答:解:(1)p1=p=75 cmHg,T1=273+27K=300K
p2=p+5cmHg=80 cmHg,T2=?
由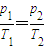 ,解得:T2=320K
,解得:T2=320K
故应使温度变为T2=320K.
(2)假设玻璃管转过180°后短臂内没有水银,水平管内留有水银柱的长度为x
P2=80cmHg,V2=V1=S?18 cm
P3=p-(10+10+10+5-x)cmHg=(40+x)cmHg,V2=S?(18+10+10-x)cm=S?(38-x)cm
由p2 V2=p3 V3,得到:80×18=(40+x)×(38-x)
解得:x=8cm,与假设相符,所以假设成立.
故密闭气体的长度变为(18+10+10-x)=30cm.
(3)密闭气体的状态变化图象如图所示.
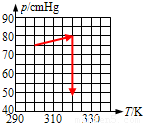
点评:利用理想气体状态方程解题,关键是正确选取状态,明确状态参量,尤其是正确求解被封闭气体的压强,这是热学中的重点知识,要加强训练,加深理解.
(2)通过假设的方法判断当玻璃管沿绕过O点的水平轴在竖直平面内逆时针转过180°时短臂内是否有水银,然后根据等温变化求解.
(3)根据两个过程中气体状态变化的特点可以画出该图象.
解答:解:(1)p1=p=75 cmHg,T1=273+27K=300K
p2=p+5cmHg=80 cmHg,T2=?
由
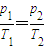 ,解得:T2=320K
,解得:T2=320K 故应使温度变为T2=320K.
(2)假设玻璃管转过180°后短臂内没有水银,水平管内留有水银柱的长度为x
P2=80cmHg,V2=V1=S?18 cm
P3=p-(10+10+10+5-x)cmHg=(40+x)cmHg,V2=S?(18+10+10-x)cm=S?(38-x)cm
由p2 V2=p3 V3,得到:80×18=(40+x)×(38-x)
解得:x=8cm,与假设相符,所以假设成立.
故密闭气体的长度变为(18+10+10-x)=30cm.
(3)密闭气体的状态变化图象如图所示.

点评:利用理想气体状态方程解题,关键是正确选取状态,明确状态参量,尤其是正确求解被封闭气体的压强,这是热学中的重点知识,要加强训练,加深理解.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 (2011?卢湾区模拟)一粗细均匀的J型玻璃管竖直放置,短臂端封闭,长臂端(足够长)开口向上,短臂内封有一定质量的理想气体.初始状态时管内各段长度如图(a)所标,密闭气体的温度为27℃.大气压强为75cmHg,求:
(2011?卢湾区模拟)一粗细均匀的J型玻璃管竖直放置,短臂端封闭,长臂端(足够长)开口向上,短臂内封有一定质量的理想气体.初始状态时管内各段长度如图(a)所标,密闭气体的温度为27℃.大气压强为75cmHg,求: (2013?德州二模)一粗细均匀的J型玻璃管竖直放置,左端封闭,右端(足够长)开口向上,左端封有一定质量的理想气体,初始状态左右两管水银面相平,如图所示.封闭气体的温度为27℃,大气压强为75cmHg.求:
(2013?德州二模)一粗细均匀的J型玻璃管竖直放置,左端封闭,右端(足够长)开口向上,左端封有一定质量的理想气体,初始状态左右两管水银面相平,如图所示.封闭气体的温度为27℃,大气压强为75cmHg.求:
