题目内容
3．某星球的质量约为地球质量的16倍，半径为地球半径的2倍，则在该星球表面的重力加速度与地球表面重力加速度的比值为（ ）| A． | 0.25 | B． | 0.5 | C． | 2 | D． | 4 |
分析 根据万有引力等于重力，得出重力加速度的表达式，结合星球质量之比和半径之比求出重力加速度之比．
解答 解：根据$G\frac{Mm}{{R}^{2}}=mg$得：g=$G\frac{M}{{R}^{2}}$，
因为星球质量为地球质量的16倍，半径为地球的2倍，则该星球表面重力加速度与地球表面重力加速度的比值为4：1．故D正确，A、B、C错误．
故选：D
点评 解决本题的关键掌握万有引力等于重力这一理论，并能灵活运用，知道重力加速度的大小与中心天体的质量和半径有关．
练习册系列答案
相关题目
13．用200N的拉力将地面上的一质量为10kg的物体提升10m（重力加速度g取10m/s2，空气阻力不计）．求：
（1）拉力对物体所做的功
（2）物体被提高后具有的重力势能
（3）物体被提高后具有的动能．
（1）拉力对物体所做的功
（2）物体被提高后具有的重力势能
（3）物体被提高后具有的动能．
14．关于曲线运动下列说法正确的是（ ）
| A． | 做曲线运动的物体，所受合外力有可能为零 | |
| B． | 曲线运动一定是变速运动 | |
| C． | 曲线运动的加速度一定变化 | |
| D． | 曲线运动的速度大小一定变化 |
如图所示，行车通过长为5米的吊臂，吊着质量为1吨的钢材，以v=2m/s速度沿水平方向匀速行驶，行车突然停车，问：
8．
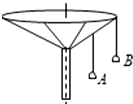如图所示，“旋转秋千”中的两个座椅A、B质量相等，通过相同长度的缆绳悬挂在旋转圆盘上．不考虑空气阻力的影响，当旋转圆盘绕竖直的中心轴匀速转动时，下列说法正确的是（ ）
如图所示，“旋转秋千”中的两个座椅A、B质量相等，通过相同长度的缆绳悬挂在旋转圆盘上．不考虑空气阻力的影响，当旋转圆盘绕竖直的中心轴匀速转动时，下列说法正确的是（ ）| A． | A与B的角速度大小相等 | |
| B． | A与B的向心加速度大小相等 | |
| C． | 悬挂A的缆绳所受的拉力比悬挂B的小 | |
| D． | 悬挂A、B的缆绳与竖直方向的夹角相等 |
如图所示，半圆玻璃砖的半径R=10cm，折射率n=$\sqrt{3}$，直径AB与屏幕MN垂直并接触于A点，激光束α以入射角i=60°射向玻璃砖圆心O，结果在屏幕MN上出现两个光斑，已知，关在真空中传播的速度为c=3×108m/s．
2．
美国物理学家劳伦斯于1932年发明的回旋加速器，应用带电粒子在磁场中做圆周运动，并使粒子在较小的空间范围内经过电场的多次加速获得较大的能量，使人类在获得较高能量带电粒子方面前进了一步，如图所示为一种改进后的回旋加速器示意图，其中盒缝间的加速电场场强大小恒定，且被限制在A、C板间，带电粒子从P0处静止释放，并沿电场线方向射入加速电场，经加速后再进入D形盒中的匀强磁场做匀速圆周运动，对于这种改进后的回旋加速器，下列说法正确的是（ ）
美国物理学家劳伦斯于1932年发明的回旋加速器，应用带电粒子在磁场中做圆周运动，并使粒子在较小的空间范围内经过电场的多次加速获得较大的能量，使人类在获得较高能量带电粒子方面前进了一步，如图所示为一种改进后的回旋加速器示意图，其中盒缝间的加速电场场强大小恒定，且被限制在A、C板间，带电粒子从P0处静止释放，并沿电场线方向射入加速电场，经加速后再进入D形盒中的匀强磁场做匀速圆周运动，对于这种改进后的回旋加速器，下列说法正确的是（ ）| A． | 带电粒子每运动一周被加速一次 | |
| B． | P1P2=P2P3 | |
| C． | 加速粒子的最大速度与D形盒的尺寸有关 | |
| D． | 加速电场方向需要做周期性的变化 |