题目内容
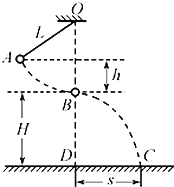
【题目】如图，一不可伸长的轻绳上端悬挂于O点，下端系一质量
的小球
现将小球拉到A点
保持绳绷直
由静止释放，当它经过B点时绳恰好被拉断，小球平抛后落在水平地面上的C点地面上的D点与OB在同一竖直线上，已知绳长
，B点离地高度
，A、B两点的高度差
，重力加速度g取
，不计空气阻力影响，求：
（1）小球在B点的速度
（2）轻绳所受的最大拉力大小
（3）地面上DC两点间的距离S．
【答案】（1）
．（2）20N．（3）
【解析】
（1）由机械能守恒定律可以求出小球到达B点的速度；
（2）在B位置，由牛顿第二定律可求轻绳所受的最大拉力大小；
（3）绳子断裂后小球做平抛运动，应用平抛运动规律可以求出s；
（1）从A到B，由机械能守恒定律得：
代入数据解得：
；
（2）小球下摆到B点时，绳的拉力和重力提供向心力，
由牛顿第二定律的：
，代入数据解的：
根据牛顿第三定律得轻绳所受的最大拉力为20N；
（3）绳子断后，小球做平抛运动，运动时间为t，
竖直方向：
，
水平方向，DC间距离：
，
代入数据解得：
；
练习册系列答案
相关题目
