题目内容
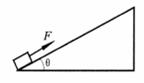
如图所示，在倾角θ＝37°的足够长的固定的斜面底端有一质量m＝1kg的物体．物体与斜面间动摩擦因数? ＝0.25，现用轻细绳将物体由静止沿斜面向上拉动．拉力F＝10N，方向平行斜面向上．经时间t＝4s绳子突然断了，求：
（1）绳断时物体的速度大小．
（2）从绳子断了开始到物体再返回到斜面底端的运动时间．（sin37°＝0.60， cos37°＝0.80，g＝10m/s2）
解：
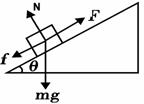
（1）在前4秒内，木块在F作用下匀加速向上运动，以沿斜面向上为正方向，受力如图，由牛顿第二定律有：
…………………….……1分
=
N …………………………………（1分）
联立以上各式可以解得：
代入数得：
…………（1分）
由速度时间公式有：
……………………（2分）
（2）木块在前4秒内发生的位移为： 
…………（1分）
绳子突然断了后，木块将匀减速至0，由牛顿第二定律有：
联立以上各式可以解得：
…………（2分）
再向上运动
…………（1分）
运动时间：
…………（1分）
之后木块沿斜面匀加速下滑回到出发点，以沿斜面向下为正方向，由受力可知
联立以上各式可以解得：
………（2分,一上两式写任意一式均得2分）
匀速下滑时间
，由
…………………….. 1分
得: 
绳断后物体运动时间：
…………（1分）
探究与巩固河南科学技术出版社系列答案
n37°＝0.6，cos37°＝0.8
