题目内容
9. 如图所示,在光滑水平地面上放置质量M=2kg的长木板,木板上表面与固定的竖直弧形轨道相切.一质量m=1kg的小滑块自A点沿弧面由静止滑下,A点距离长木板上表面高度h=0.6m.滑块在木板上滑行t=1s后,和木板以共同速度v=1m/s匀速运动,取g=10m/s2.求:
如图所示,在光滑水平地面上放置质量M=2kg的长木板,木板上表面与固定的竖直弧形轨道相切.一质量m=1kg的小滑块自A点沿弧面由静止滑下,A点距离长木板上表面高度h=0.6m.滑块在木板上滑行t=1s后,和木板以共同速度v=1m/s匀速运动,取g=10m/s2.求:(1)滑块与木板间的摩擦力.
(2)滑块沿弧面下滑过程中克服摩擦力做的功.
(3)滑块相对木板滑行的距离及在木板上产生的热量.
分析 (1)滑块滑上木板后,木块做匀减速直线运动,木板做匀加速直线运动,根据速度时间公式求出木板的加速度,根据牛顿第二定律求出滑块与木板间的摩擦力.
(2)根据动量守恒定律求出滑块的初速度,根据动能定理求出滑块沿弧面下滑过程中克服摩擦力做的功.
(3)根据能量守恒定律求出滑块相对木板滑行的距离,以及产生的热量.
解答 解:(1)根据匀变速直线运动的速度时间公式得木板的加速度为:a=$\frac{v}{t}$=$\frac{1}{1}$=1m/s2.
以木板为研究对象,根据牛顿第二定律得,滑块与木板间的摩擦力为:f=Ma=2N.
(2)取向右为正方向,根据动量守恒定律得:mv0=(M+m)v
解得:v0=$\frac{(M+m)v}{m}$=$\frac{(2+1)×1}{1}$m/s=3m/s.
滑块沿弧面下滑的过程,根据动能定理得:
mgh-Wf=$\frac{1}{2}$mv02-0
代入数据解得:Wf=1.5J.
(3)根据能量守恒定律得:f△x=$\frac{1}{2}$mv02-$\frac{1}{2}$(M+m)v2
解得滑块相对木板滑行的距离为:△x=1.5m.
产生的热量为:Q=f△x=2×1.5J=3J
答:(1)滑块与木板间的摩擦力为2N.
(2)滑块沿弧面下滑过程中克服摩擦力做的功为1.5J.
(3)滑块相对木板滑行的距离为1.5m,在木板上产生的热量是3J.
点评 本题考查对不同研究对象进行受力分析,并由运动学规律求出加速度,根据牛顿第二定律来确定摩擦力大小.要知道求产生热量也可能用动能定理来求解.

练习册系列答案
 寒假乐园北京教育出版社系列答案
寒假乐园北京教育出版社系列答案
相关题目
19.机动车的尾气含有铅等大量有害物质,并且也是造成地球“温室效应”的重要因素之一.电动汽车因其无尾气排放且噪音小等因素,正在逐渐被人们接受.某国产品牌电动汽车的铭牌如下,已知蓄电池储存的电能等于其容量乘输出电压,则下列说法正确的是( )
| 规格 | 后轮驱动直流电动机 |
| 车型:60″电动汽车 | 电动机额定输出功率:1675W |
| 整车质量:400kg | 额定转速:600r/min |
| 蓄电池(容量It=800Ah,输出电压:U≥36V) | 额定工作电压/电流:36V/50A |
| A. | 电动汽车正常工作时消耗的电功率1675W | |
| B. | 电动机的内阻为0.5Ω | |
| C. | 蓄电池充满电后储存的电能不小于2.88×104J | |
| D. | 充满电后在额定功率下连续行驶的时间不小于16h |
20.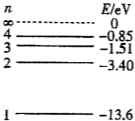 图示为氢原子的能级图.现有大量处于n=4能级的氢原子向低能级跃迁,并辐射出光子.下列说法正确的是( )
图示为氢原子的能级图.现有大量处于n=4能级的氢原子向低能级跃迁,并辐射出光子.下列说法正确的是( )
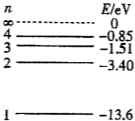 图示为氢原子的能级图.现有大量处于n=4能级的氢原子向低能级跃迁,并辐射出光子.下列说法正确的是( )
图示为氢原子的能级图.现有大量处于n=4能级的氢原子向低能级跃迁,并辐射出光子.下列说法正确的是( )| A. | 该群氢原子向低能级跃迁时,最多可能辐射出6种不同频率的光 | |
| B. | 该群氢原子向低能级路迁时,辐射出光子能量的最大值为0.85eV | |
| C. | 该群氢原子由n=4能级跃迁到n=1能级产生的光频率最高 | |
| D. | 若由n=3能级跃迁到n=2能级产生的光能使某种金属逸出光电子,则由n=2能级跃迁到n=1能级产生的光也一定能使该种金属逸出光电子 | |
| E. | 若由n=4能级跃迁到n=2能级,由n=3能级跃迁到n=2能级和由n=4能级跃迁到n=3能级产生的光的波长分别为λ1、λ2、λ3,则λ1=λ2+λ3 |
17. 某种金属逸出光电子的虽大初动能E.与入射光频率v的关系如图所示,其中№为极限频率.从图中可以确定的是( )
某种金属逸出光电子的虽大初动能E.与入射光频率v的关系如图所示,其中№为极限频率.从图中可以确定的是( )
 某种金属逸出光电子的虽大初动能E.与入射光频率v的关系如图所示,其中№为极限频率.从图中可以确定的是( )
某种金属逸出光电子的虽大初动能E.与入射光频率v的关系如图所示,其中№为极限频率.从图中可以确定的是( )| A. | Ekm与入射光强度成正比 | |
| B. | 图中直线的斜率与昔朗克常量有关 | |
| C. | 光电子的逸出功与入射光频率v无关 | |
| D. | 当v<v0时,无论入射光强度多大都不会逸出光电子 | |
| E. | 当v<v0时,只要入射光强度足够强也会逸出光电子 |
4.下列说法中正确的是( )
| A. | 气体分子的平均速率增大,气体的压强也一定增大 | |
| B. | 叶面上的小露珠呈球形是由于液体表面张力的作用 | |
| C. | 液晶的光学性质与某些晶体相似,具有各向异性 | |
| D. | 因为布朗运动的激烈程度与温度有关,所以布朗运动也叫做热运动 |
14.对于光电效应的研究结果,下列叙述中$\underset{不}{•}$$\underset{正}{•}$$\underset{确}{•}$的是( )
| A. | 光电子的发射几乎是瞬时的 | |
| B. | 入射光的频率必须大于极限频率时才能产生光电效应 | |
| C. | 发生光电效应时,单位时间里照射到金属表面的光子数目越多,则单位时间内从金属表面逸出的光电子数会越多 | |
| D. | 发生光电效应时,从金属表面逸出的光电子的速度大小均相等 |
18.将物体以某一初速度υ0竖直向上抛出,在0-t1时间内运动的位移时间图象和速度时间图象如图所示,不计空气阻力,重力加速度g=10m/s2,则( )


| A. | υ0=32m/s | B. | t1=2s | ||
| C. | 物体上升的最大高度为37.8m | D. | 物体0-t1时间内平均速度为21m/s |
 图中帆板船的帆与船身成37°角,今有垂直于帆,大小为400N的风力作用于帆面上,则船在前进方向上获得的推力为240N,在船的侧面所受的推力为320N.
图中帆板船的帆与船身成37°角,今有垂直于帆,大小为400N的风力作用于帆面上,则船在前进方向上获得的推力为240N,在船的侧面所受的推力为320N. 一个初始质量为1.00kg的玩具火箭被竖直发射到空中,它的质量以0.20kg•s-1的恒定速率减小,火箭最终质量为0.20kg,喷出的气体对火箭的推力随时间变化的规律如图所示,火箭所经处重力加速度恒为10m•s-2.
一个初始质量为1.00kg的玩具火箭被竖直发射到空中,它的质量以0.20kg•s-1的恒定速率减小,火箭最终质量为0.20kg,喷出的气体对火箭的推力随时间变化的规律如图所示,火箭所经处重力加速度恒为10m•s-2.