题目内容
如图所示，在x＜0的区域内存在沿y轴负方向的匀强电场，在第一象限倾斜直线OM的下方和第四象限内存在垂直纸面向里的匀强磁场。一带电粒子自电场中的P点沿x轴正方向射出，恰好经过坐标原点O进入匀强磁场，经磁场偏转后垂直于y轴从N点回到电场区域，并恰能返回P点。已知P点坐标为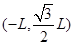
，带电粒子质量为m，电荷量为q，初速度为v0，不计粒子重力。求：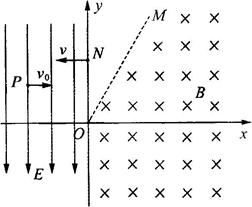
（1）匀强电场的电场强度大小；
（2）N点的坐标；
（3）匀强磁场的磁感应强度大小。
（1）
（2）（0，
） （3）
解析试题分析：（1）设粒子从P到O时间为t，加速度为a，则
由牛顿第二定律，可得
由以上三式，可解得
（2）设粒子运动到N点时速度为v，则 
所以粒子从N到P的时间
沿y轴位移 
因此N点坐标为（0，）
(3)粒子在磁场中运动轨迹如图所示，设半径为R。
粒子在O点时速度方向与y轴负方向的夹角为30º
由几何关系可知 
又因为 
解得 
考点：
练习册系列答案
相关题目
如图所示，做匀速直线运动的小车A通过一根绕过定滑轮的长绳吊起一重物B，设重物和小车速度的大小分别为vB、vA，则
| A．vA>vB |
| B．vA<vB |
| C．绳的拉力大于B的重力 |
| D．绳的拉力等于B的重力 |
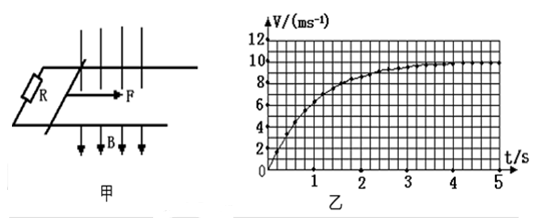
U时，x轴上开始出现荧光。（不计电子的重力）试求：
；
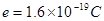，电子质量
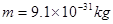。求：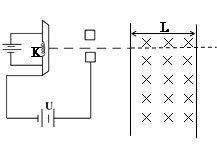
)
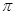