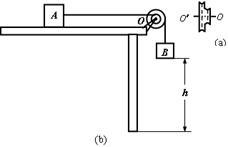
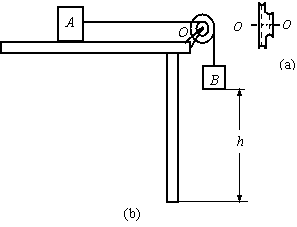
题目内容
 线轮的两部分半径不同(其侧视图如图a所示),大轮半径R=10cm,小轮半径r=5cm.线轮可绕固定支架上的光滑水平轴OO′转动,小轮通过细绳与放在水平桌面上的物体A相连,大轮通过细线与物体B相连,如图b所示.A、B质量分别为mA=4kg、mB=0.75kg,A与桌面间的动摩擦因数μ=0.5,B的下表面距地面高h=1m.不计细绳和线轮的质量,整个系统处于静止状态.(g=10m/s2)求:
线轮的两部分半径不同(其侧视图如图a所示),大轮半径R=10cm,小轮半径r=5cm.线轮可绕固定支架上的光滑水平轴OO′转动,小轮通过细绳与放在水平桌面上的物体A相连,大轮通过细线与物体B相连,如图b所示.A、B质量分别为mA=4kg、mB=0.75kg,A与桌面间的动摩擦因数μ=0.5,B的下表面距地面高h=1m.不计细绳和线轮的质量,整个系统处于静止状态.(g=10m/s2)求:(1)物体A所受到的静摩擦力大小.
(2)将物体B换成一个大小相同,质量为原来两倍的物体B′后,整个系统由静止开始运动,当物体B′落到地面的瞬间,物体A的速度大小.
(3)在(2)描述的情况下,B′从开始运动至落地的时间.
分析:(1)对轮轴运用力矩平衡条件列式求解即可;
(2)对A与B系统运用动能定理列式,根据公式v=ωr得到A、B的线速度关系,然后联立求解即可;
(3)物体B做初速度为零的匀加速直线运动,根据运动学公式列式求解.
(2)对A与B系统运用动能定理列式,根据公式v=ωr得到A、B的线速度关系,然后联立求解即可;
(3)物体B做初速度为零的匀加速直线运动,根据运动学公式列式求解.
解答:解:(1)设水平细绳张力大小为TA,竖直细绳张力大小为TB.以OO’转轴,线轮处于力矩平衡状态,有
TAr=TBR
又TB=mBg
解得TA=
mBg=
×0.75×10N=15N
由于物体A静止,它所受到的静摩擦力大小为fA=TA=15N
(2)对整个系统,由动能定理mB′gh-μmAgsA=
mB′vB2+
mAvA2
由于
=
,所以有sA=
h,
vB=2vA
可解得vA=
=
m/s=1m/s
(3)由于B所受的重力不变,A所受的摩擦力不变,所以A、B均做匀加速直线运动.
由(2)可得B′落地时的速度为vB=2vA=2m/s
故B′运动的平均速度为
B=
=1m/s
t=
=
s=1s
答:(1)物体A所受到的静摩擦力大小为15N.
(2)物体A的速度大小为1m/s.
(3)物体B′从开始运动至落地的时间为1s.
TAr=TBR
又TB=mBg
解得TA=
| R |
| r |
| 0.10 |
| 0.05 |
由于物体A静止,它所受到的静摩擦力大小为fA=TA=15N
(2)对整个系统,由动能定理mB′gh-μmAgsA=
| 1 |
| 2 |
| 1 |
| 2 |
由于
| r |
| R |
| 1 |
| 2 |
| 1 |
| 2 |
vB=2vA
可解得vA=
|
|
(3)由于B所受的重力不变,A所受的摩擦力不变,所以A、B均做匀加速直线运动.
由(2)可得B′落地时的速度为vB=2vA=2m/s
故B′运动的平均速度为
. |
| v |
| vB |
| 2 |
t=
| h | ||
|
| 1 |
| 1 |
答:(1)物体A所受到的静摩擦力大小为15N.
(2)物体A的速度大小为1m/s.
(3)物体B′从开始运动至落地的时间为1s.
点评:本题关键根据力矩平衡条件列式求解出静摩擦力;对物体系统运用动能定理列式求解出落地速度;最后根据运动学公式列式求解.

练习册系列答案
 期末1卷素质教育评估卷系列答案
期末1卷素质教育评估卷系列答案
相关题目