题目内容
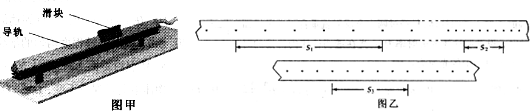
 如图所示,轻杆一端固定一个光滑小球,杆的转动轴O点固定在竖直墙上(杆可绕O点在竖直平面内无摩擦转动),小球同时搁置在光滑斜面上,杆与竖直墙面夹角为α,斜面倾角为β.初始时α<β且(α+β)<90°.为使斜面能在光滑地面上保持匀速运动(小球不离开斜面),作用在斜面上的水平外力F的大小以及轻杆受力T的大小变化,下列判断正确的是
如图所示,轻杆一端固定一个光滑小球,杆的转动轴O点固定在竖直墙上(杆可绕O点在竖直平面内无摩擦转动),小球同时搁置在光滑斜面上,杆与竖直墙面夹角为α,斜面倾角为β.初始时α<β且(α+β)<90°.为使斜面能在光滑地面上保持匀速运动(小球不离开斜面),作用在斜面上的水平外力F的大小以及轻杆受力T的大小变化,下列判断正确的是
- A.F逐渐增大,T逐渐减小
- B.F逐渐增大,T先减小后增大
- C.F逐渐增大,T先增大后减小
- D.F逐渐减小,T逐渐增大
B
分析:先对小球受力分析,根据共点力平衡条件列式求出支持力和杆的弹力的表达式;再对斜面体受力分析,根据共点力平衡条件求出地面支持力和推力的表达式,最后分析讨论.
解答:对小球受力分析,受到重力mg、支持力N和杆的支持力T,如图

根据共点力平衡条件,有 =
= =
=
解得
N= mg=
mg=
T= mg
mg
对斜面体受力分析,受到推力F、重力Mg、支持力FN和压力N,如图

根据共点力平衡条件,有
Nsinβ=F
解得
F=Nsinβ= mg=
mg=
故随着α的增大,T先减小后增大,F增大
故选B.
点评:本题关键是先对小球受力分析,再对斜面体受力分析,然后根据平衡条件,运用合成法列式求解出各个力的表达式,再进行讨论.
分析:先对小球受力分析,根据共点力平衡条件列式求出支持力和杆的弹力的表达式;再对斜面体受力分析,根据共点力平衡条件求出地面支持力和推力的表达式,最后分析讨论.
解答:对小球受力分析,受到重力mg、支持力N和杆的支持力T,如图

根据共点力平衡条件,有
 =
= =
=
解得
N=
 mg=
mg=
T=
 mg
mg对斜面体受力分析,受到推力F、重力Mg、支持力FN和压力N,如图

根据共点力平衡条件,有
Nsinβ=F
解得
F=Nsinβ=
 mg=
mg=
故随着α的增大,T先减小后增大,F增大
故选B.
点评:本题关键是先对小球受力分析,再对斜面体受力分析,然后根据平衡条件,运用合成法列式求解出各个力的表达式,再进行讨论.

练习册系列答案
相关题目
 如图所示,一质量为m的小球套在光滑竖直杆上,轻质弹簧一端固定于O点,另一端与该小球相连.现将小球从A点由静止释放,沿竖直杆运动到B点,已知OA长度小于OB长度,弹簧处于OA、OB两位置时弹力大小相等.在小球由A到B的过程中( )
如图所示,一质量为m的小球套在光滑竖直杆上,轻质弹簧一端固定于O点,另一端与该小球相连.现将小球从A点由静止释放,沿竖直杆运动到B点,已知OA长度小于OB长度,弹簧处于OA、OB两位置时弹力大小相等.在小球由A到B的过程中( )| A、加速度等于重力加速度g的位置有两个 | B、弹簧弹力的功率为零的位置有两个 | C、弹簧弹力对小球所做的正功等于小球克服弹簧弹力所做的功 | D、弹簧弹力做正功过程中小球运动的距离等于小球克服弹簧弹力做功过程中小球运动的距离 |
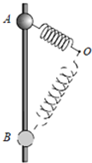 如图所示,一质量为m的小球套在光滑竖直杆上,轻质弹簧一端固定于O点,另一端与该小球相连,小球在A处时弹簧处于压缩状态.现将小球从A点由静止释放,沿竖直杆运动到B点,已知OA长度小于OB长度,弹簧处于OA、OB两位置时弹力大小相等.在小球由A到B的过程中( )
如图所示,一质量为m的小球套在光滑竖直杆上,轻质弹簧一端固定于O点,另一端与该小球相连,小球在A处时弹簧处于压缩状态.现将小球从A点由静止释放,沿竖直杆运动到B点,已知OA长度小于OB长度,弹簧处于OA、OB两位置时弹力大小相等.在小球由A到B的过程中( )| A、加速度大小等于重力加速度g的位置有两个 | B、小球运动到与O点等高的位置时,弹簧弹力的功率不为零 | C、弹簧弹力对小球先做正功再做负功 | D、小球到达B点时的速度一定为零 |
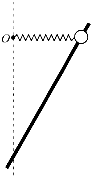 如图所示,质量为m的小球套在倾斜放置的固定光滑杆上,一根轻质弹簧一端固定于O点,另一端与小球相连,弹簧与杆在同一竖直平面内,将小球沿杆拉到弹簧水平位置由静止释放,小球沿杆下滑,当弹簧位于竖直位置时,小球速度恰好为零,此时小球下降的竖直高度为h,若全过程中弹簧始终处于伸长状态且处于弹性限度范围内,下列说法正确的是( )
如图所示,质量为m的小球套在倾斜放置的固定光滑杆上,一根轻质弹簧一端固定于O点,另一端与小球相连,弹簧与杆在同一竖直平面内,将小球沿杆拉到弹簧水平位置由静止释放,小球沿杆下滑,当弹簧位于竖直位置时,小球速度恰好为零,此时小球下降的竖直高度为h,若全过程中弹簧始终处于伸长状态且处于弹性限度范围内,下列说法正确的是( )| A、弹簧与杆垂直时,小球速度最大 | B、弹簧与杆垂直时,小球的动能与重力势能之和最大 | C、小球下滑至最低点的过程中,弹簧的弹性势能增加量小于mgh | D、小球下滑至最低点的过程中,弹簧的弹性势能增加量等于mgh |
 在弹性限度内,弹簧弹力的大小与弹簧伸长(或缩短)的长度的比值,叫做弹簧的劲度系数.为了测量一轻弹簧的劲度系数,某同学进行了如下实验设计:如图所示,将两平行金属导轨水平固定在竖直向下的匀强磁场中,金属杆ab与导轨接触良好,水平放置的轻弹簧一端固定于O点,另一端与金属杆连接并保持绝缘.在金属杆滑动的过程中,弹簧与金属杆、金属杆与导轨均保持垂直,弹簧的形变始终在弹性限度内,通过减小金属杆与导轨之间的摩擦和在弹簧的形变较大时读数等方法,使摩擦对实验结果的影响可忽略不计.
在弹性限度内,弹簧弹力的大小与弹簧伸长(或缩短)的长度的比值,叫做弹簧的劲度系数.为了测量一轻弹簧的劲度系数,某同学进行了如下实验设计:如图所示,将两平行金属导轨水平固定在竖直向下的匀强磁场中,金属杆ab与导轨接触良好,水平放置的轻弹簧一端固定于O点,另一端与金属杆连接并保持绝缘.在金属杆滑动的过程中,弹簧与金属杆、金属杆与导轨均保持垂直,弹簧的形变始终在弹性限度内,通过减小金属杆与导轨之间的摩擦和在弹簧的形变较大时读数等方法,使摩擦对实验结果的影响可忽略不计.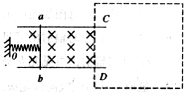 (1)在弹性限度内,弹簧弹力的大小与弹簧伸长(或缩短)的长度的比值,叫做弹簧的劲度系数.为了测量一轻弹簧的劲度系数,某同学进行了如下实验设计:如图所示,将两平行金属导轨水平固定在竖直向下的匀强磁场中,金属杆ab与导轨接触良好,水平放置的轻弹簧一端固定于O点,另一端与金属杆连接并保持绝缘.在金属杆滑动的过程中,弹簧与金属杆、金属杆与导轨均保持垂直,弹簧的形变始终在弹性限度内,通过减小金属杆与导轨之间的摩擦和在弹簧形变较大时读数等方法,使摩擦对实验结果的影响可忽略不计.
(1)在弹性限度内,弹簧弹力的大小与弹簧伸长(或缩短)的长度的比值,叫做弹簧的劲度系数.为了测量一轻弹簧的劲度系数,某同学进行了如下实验设计:如图所示,将两平行金属导轨水平固定在竖直向下的匀强磁场中,金属杆ab与导轨接触良好,水平放置的轻弹簧一端固定于O点,另一端与金属杆连接并保持绝缘.在金属杆滑动的过程中,弹簧与金属杆、金属杆与导轨均保持垂直,弹簧的形变始终在弹性限度内,通过减小金属杆与导轨之间的摩擦和在弹簧形变较大时读数等方法,使摩擦对实验结果的影响可忽略不计.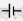 )、滑动变阻器(
)、滑动变阻器(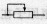 )、电流表(
)、电流表(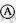 )、开关(
)、开关(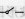 )设计一电路图,画在图中虚线框内,并正确连在导轨的C、D两端.
)设计一电路图,画在图中虚线框内,并正确连在导轨的C、D两端.