题目内容
 在固定的光滑水平杆(杆足够长)上,套有一个质量m=0.5kg的光滑金属圆环,
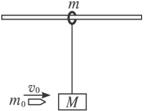
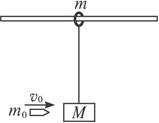
在固定的光滑水平杆(杆足够长)上,套有一个质量m=0.5kg的光滑金属圆环,一长为L=1m的轻绳,一端拴在环上,另一端系着一个质量为M=2kg的木块,如图所示.现有一质量为m=20g的子弹以V=1000m/s的水平速度射穿木块,子弹穿出木块后的速度为u=200m/s(不计空气阻力和子弹与木块作用的时间),试问:
(1)当子弹射穿木块后,木块向右摆动的最大高度为多大?
(2)当木块第一次返回到最低点时,木块的速度是多大?
【答案】分析:(1)子弹射穿木块的过程遵守动量守恒,由动量守恒定律求出子弹穿出木块后木块的速度.木块与圆环一起向右摆动的过程中,系统水平方向不受外力,水平方向动量守恒.当两者水平速度相同时向右摆到最大高度,由动量守恒和机械能守恒结合求解木块向右摆动的最大高度.
(2)木块从最高点返回最低点的过程中,满足水平方向动量守恒和机械能守恒,再由两大守恒定律列方程求解木块第一次返回到最低点时的速度.
解答:解:(1)设子弹从木块穿过后木块获得的速度为v,根据动量守恒得
mv=mu+Mv
代入解得v=8m/s
木块与圆环一起向右摆动的过程中,由水平方向动量守恒和机械能守恒得
Mv=(M+m)v1
 =
= +(M+m)h
+(M+m)h
解得h=0.64m
(3)整个过程,由水平方向动量守恒和机械能守恒得
Mv=Mv2+mv3
 =
= +
+
解得,v2=4.8m/s,v3=12.8m/s
v2=8m/s,v3=0
在木块摆动的过程中,圆环一直受水平向右的绳子的分力作用,速度一直增大,所以v3=0不可能,舍去.
答:
(1)当子弹射穿木块后,木块向右摆动的最大高度为0.64m.
(2)当木块第一次返回到最低点时,木块的速度是4.8m/s.
点评:本题是连接体机械能守恒和水平方向动量守恒问题,研究对象只能针对系统,对单个物体机械能不守恒.
(2)木块从最高点返回最低点的过程中,满足水平方向动量守恒和机械能守恒,再由两大守恒定律列方程求解木块第一次返回到最低点时的速度.
解答:解:(1)设子弹从木块穿过后木块获得的速度为v,根据动量守恒得
mv=mu+Mv
代入解得v=8m/s
木块与圆环一起向右摆动的过程中,由水平方向动量守恒和机械能守恒得
Mv=(M+m)v1
 =
= +(M+m)h
+(M+m)h解得h=0.64m
(3)整个过程,由水平方向动量守恒和机械能守恒得
Mv=Mv2+mv3
 =
= +
+
解得,v2=4.8m/s,v3=12.8m/s
v2=8m/s,v3=0
在木块摆动的过程中,圆环一直受水平向右的绳子的分力作用,速度一直增大,所以v3=0不可能,舍去.
答:
(1)当子弹射穿木块后,木块向右摆动的最大高度为0.64m.
(2)当木块第一次返回到最低点时,木块的速度是4.8m/s.
点评:本题是连接体机械能守恒和水平方向动量守恒问题,研究对象只能针对系统,对单个物体机械能不守恒.

练习册系列答案
相关题目
 在固定的光滑水平杆(杆足够长)上,套有一个质量m=0.5kg的光滑金属圆环,
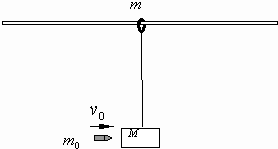
在固定的光滑水平杆(杆足够长)上,套有一个质量m=0.5kg的光滑金属圆环, (2013?商丘三模)如图所示,在固定的光滑水平杆(杆足够长)上,套有一个质量为m=0.5kg的光滑金属圆环,轻绳一端拴在环上,另一端系着一个质量为M=1.98kg的木块,现有一质量为m0=20g的子弹以v0=100m/s的水平速度射入木块并留在木块中(不计空气阻力和子弹与木块作用的时间,g取10m/s2),求:
(2013?商丘三模)如图所示,在固定的光滑水平杆(杆足够长)上,套有一个质量为m=0.5kg的光滑金属圆环,轻绳一端拴在环上,另一端系着一个质量为M=1.98kg的木块,现有一质量为m0=20g的子弹以v0=100m/s的水平速度射入木块并留在木块中(不计空气阻力和子弹与木块作用的时间,g取10m/s2),求: