题目内容
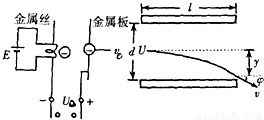
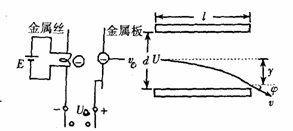
如图所示,设从灼热金属丝逸出的电子流初速为零,并设该电子流,经加速后进入偏转电场.已知加速电场的电压是U0,偏转极板间的电压是U,偏转板长L,相距d,电子电量为e,质量为m.求:
(1)电子进入偏转电场时的速度v0大小;A
(2)电子离开偏转电场时的侧移距离y;
(3)电子离开偏转电场时的速度v大小.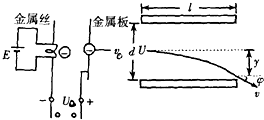
(1)电子进入偏转电场时的速度v0大小;A
(2)电子离开偏转电场时的侧移距离y;
(3)电子离开偏转电场时的速度v大小.

(1)电子在加速电场中运动时只有电场力做功,
由动能定理得:eu0=
mv02
解得:v0=
(2)电子离开偏转电场后做类平抛运动,水平方向匀速,竖直方向初速度为零的匀加速运动;
水平:L=v0t
竖直:y=
at2
解得:y=
(
)2=
(3)由于竖直方向初速度为零的匀加速运动;
所以:vy=at=
v=
=
=
由动能定理:e
y=
mv2-
mv02
解得:v=
答:(1)电子进入偏转电场时的速度v0大小为v0=
.
(2)电子离开偏转电场时的侧移距离为
.
(3)电子离开偏转电场时的速度v大小为
.
由动能定理得:eu0=
| 1 |
| 2 |
解得:v0=
|
(2)电子离开偏转电场后做类平抛运动,水平方向匀速,竖直方向初速度为零的匀加速运动;
水平:L=v0t
竖直:y=
| 1 |
| 2 |
解得:y=
| 1 |
| 2 |
| eu |
| md |
| L |
| v0 |
| L2u |
| 4u0d |
(3)由于竖直方向初速度为零的匀加速运动;
所以:vy=at=
| euL |
| mdv0 |
v=
| v02+vy2 |
|
|
由动能定理:e
| u |
| d |
| 1 |
| 2 |
| 1 |
| 2 |
解得:v=
|
答:(1)电子进入偏转电场时的速度v0大小为v0=
|
(2)电子离开偏转电场时的侧移距离为
| L2u |
| 4u0d |
(3)电子离开偏转电场时的速度v大小为
|

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
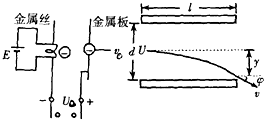 如图所示,设从灼热金属丝逸出的电子流初速为零,并设该电子流,经加速后进入偏转电场.已知加速电场的电压是U0,偏转极板间的电压是U,偏转板长L,相距d,电子电量为e,质量为m.求:
如图所示,设从灼热金属丝逸出的电子流初速为零,并设该电子流,经加速后进入偏转电场.已知加速电场的电压是U0,偏转极板间的电压是U,偏转板长L,相距d,电子电量为e,质量为m.求: