题目内容
物体做匀速圆周运动,轨道半径R=2m,运动周期T=4s,则物体的线速度为 m/s,角速度为 rad/s,向心加速度大小为 m/s2,任意1s内物体的位移大小为 m.
【答案】分析:根据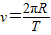 求线速度;由
求线速度;由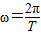 可求出角速度;根据a=rω2求运动的向心加速度.由周期与半径可求出任意1秒内的位移大小.
可求出角速度;根据a=rω2求运动的向心加速度.由周期与半径可求出任意1秒内的位移大小.
解答:解:根据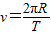 ,则线速度
,则线速度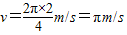 ;
;
由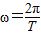 ,则角速度为
,则角速度为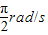 ;
;
根据a=rω2,则运动的向心加速度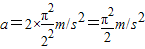 .
.
由周期与半径,则任意1秒内路程为 圆弧,则其位移大小
圆弧,则其位移大小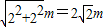 .
.
故答案为:π,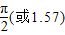 ,
, ,
,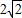
点评:解决本题的关键掌握线速度与角速度的关系,以及掌握向心加速度与线速度、角速度的关系.并区别位移与路程的不同,同时会求出位移的大小.
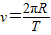 求线速度;由
求线速度;由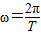 可求出角速度;根据a=rω2求运动的向心加速度.由周期与半径可求出任意1秒内的位移大小.
可求出角速度;根据a=rω2求运动的向心加速度.由周期与半径可求出任意1秒内的位移大小.解答:解:根据
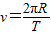 ,则线速度
,则线速度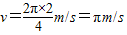 ;
;由
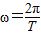 ,则角速度为
,则角速度为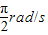 ;
;根据a=rω2,则运动的向心加速度
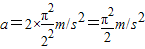 .
.由周期与半径,则任意1秒内路程为
 圆弧,则其位移大小
圆弧,则其位移大小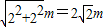 .
.故答案为:π,
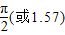 ,
, ,
,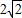
点评:解决本题的关键掌握线速度与角速度的关系,以及掌握向心加速度与线速度、角速度的关系.并区别位移与路程的不同,同时会求出位移的大小.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 如图所示,小物块m与圆盘保持相对静止,并随圆盘一起做匀速圆周运动,则小物块 的受力情况是( )
如图所示,小物块m与圆盘保持相对静止,并随圆盘一起做匀速圆周运动,则小物块 的受力情况是( )