题目内容
一质量为M=2kg的小物块随足够长的水平传送带一起向右运动,被一水平向左飞来的子弹击中,子弹从物块中瞬时穿过,如图甲所示,地面观察者记录了小物块被击中后的速度随时间的变化关系,如图乙所示(图中取向右运动的方向为正方向),已知传送带的速度保持不变,(g取10m/s2)

(1)计算物块与传送带间的动摩擦系数?
(2)摩擦力对物块做的功是多少?
(3)系统有多少能量转化为内能?

(1)计算物块与传送带间的动摩擦系数?
(2)摩擦力对物块做的功是多少?
(3)系统有多少能量转化为内能?
分析:(1)计算物块与传送带之间的摩擦因数,首先从图象中找出物体仅在摩擦力作用下运动时加速度,后由牛顿第二定律摩擦力即可求出 μ.
(2)根据动能定理,传送带对小物块所做的功即小物块的动能变化.
(3)为了求出由于摩擦产生的内能,必须得到由于摩擦物体与传送带之间相对的路程,本题应该分两段来讨论,第一段物体与传送带向不同的方向运动,相对路程为他们相对地面路程的和;第二段物体与传送带同向运动,相对路程为他们相对地面路程的差.摩擦力与相对路程的乘积即为产生的内能.
(2)根据动能定理,传送带对小物块所做的功即小物块的动能变化.
(3)为了求出由于摩擦产生的内能,必须得到由于摩擦物体与传送带之间相对的路程,本题应该分两段来讨论,第一段物体与传送带向不同的方向运动,相对路程为他们相对地面路程的和;第二段物体与传送带同向运动,相对路程为他们相对地面路程的差.摩擦力与相对路程的乘积即为产生的内能.
解答:解:(1)小物块最后与传送带的运动速度相同,从图象上可读出小物块的末速度速度v的大小为2.0m/s.小物块的初速度v0=-4m/s.
小物块在滑动摩擦力的作用下做匀变速运动的加速度为a=
=
m/s2=2.0m/s2,
由牛顿第二定律得:f=μMg=Ma
得到小物块与传送带之间的动摩擦因数:μ=
=0.2
(2)从子弹离开小物块到小物块与传送带一起匀速运动的过程中,设传送带对小物块所做的功为W,
由动能定理得:W=△Ek=
mv2-
m
=
×2×[22-(-4)2]J=-12J.
即传送带对小物块做负功,大小为12J.
(3)由速度图象可知,传送带与物块存在摩擦力的时间只有3秒,
0~2s内:s物1=
a
=
×2×22m=4m;(向左) s带1=vt1=2×2m=4m,(向右);
2~3s内:s物2=
a
=
×2×12m=1m,(向右); s带2=vt2=2×1m=2m,(向右);
所以,物块与传送带之间的相对位移△S相=(4m+4m)+(2m-1m)=9m
产生的内能 Q=f?S相=μMg S相=0.2×2.0×10×9=36(J)
答:(1)小物块与传送带之间的动摩擦因数μ=0.2;
(2)传送带对小物块做负功,大小为12J;
(3)物块与传送带之间由于摩擦而产生的内能Q=36J.
小物块在滑动摩擦力的作用下做匀变速运动的加速度为a=
| △v |
| △t |
| 2-(-4) |
| 3 |
由牛顿第二定律得:f=μMg=Ma
得到小物块与传送带之间的动摩擦因数:μ=
| Ma |
| Mg |
(2)从子弹离开小物块到小物块与传送带一起匀速运动的过程中,设传送带对小物块所做的功为W,
由动能定理得:W=△Ek=
| 1 |
| 2 |
| 1 |
| 2 |
| v | 2 0 |
| 1 |
| 2 |
即传送带对小物块做负功,大小为12J.
(3)由速度图象可知,传送带与物块存在摩擦力的时间只有3秒,
0~2s内:s物1=
| 1 |
| 2 |
| t | 2 1 |
| 1 |
| 2 |
2~3s内:s物2=
| 1 |
| 2 |
| t | 2 2 |
| 1 |
| 2 |
所以,物块与传送带之间的相对位移△S相=(4m+4m)+(2m-1m)=9m
产生的内能 Q=f?S相=μMg S相=0.2×2.0×10×9=36(J)
答:(1)小物块与传送带之间的动摩擦因数μ=0.2;
(2)传送带对小物块做负功,大小为12J;
(3)物块与传送带之间由于摩擦而产生的内能Q=36J.
点评:考查了v-t图象,理解图象的物理意义,牛顿运动定律结合动能定理的综合应用.

练习册系列答案
相关题目
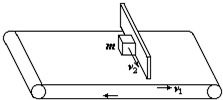 一质量为m=2kg的物体置于水平传送带上,随传送带一起以速度v1=2.0m/s向前运动,中途因受到一光滑挡板的阻碍而停止向前运动;现要用一平行于挡板的水平力F将物体以速度v2=1.5m/s沿着挡板拉离传送带,已知板与传送带运动方向垂直(如图所示),物体与传送带间的动摩擦因数为μ=0.3,试求拉力F和挡板对物体的弹力N的大小.
一质量为m=2kg的物体置于水平传送带上,随传送带一起以速度v1=2.0m/s向前运动,中途因受到一光滑挡板的阻碍而停止向前运动;现要用一平行于挡板的水平力F将物体以速度v2=1.5m/s沿着挡板拉离传送带,已知板与传送带运动方向垂直(如图所示),物体与传送带间的动摩擦因数为μ=0.3,试求拉力F和挡板对物体的弹力N的大小. 如图所示,水平的传送带以初速度v0=2m/s,加速度
如图所示,水平的传送带以初速度v0=2m/s,加速度
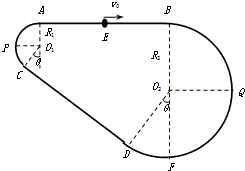 如图是放置在竖直平面内游戏滑轨的模拟装置,滑轨由四部分粗细均匀的金属杆组成:水平直轨AB,半径分别为R1=1.0m和R2=3.0m的弧形轨道,倾斜直轨CD长为L=6m,AB、CD与两圆形轨道相切,其中倾斜直轨CD部分表面粗糙,动摩擦因数为μ=
如图是放置在竖直平面内游戏滑轨的模拟装置,滑轨由四部分粗细均匀的金属杆组成:水平直轨AB,半径分别为R1=1.0m和R2=3.0m的弧形轨道,倾斜直轨CD长为L=6m,AB、CD与两圆形轨道相切,其中倾斜直轨CD部分表面粗糙,动摩擦因数为μ=