题目内容
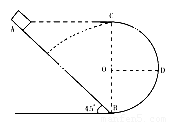
(12分)如图所示,倾角为45°的粗糙斜面AB底端与半径R=0.4m的光滑半圆轨道BC平滑相接,O为轨道圆心,BC为圆轨道直径且处于竖直平面内,A、C两点等高。质量m=1kg的滑块(可视为质点)从A点由静止开始下滑,恰能滑到与O等高的D点,g取10m/s2。
(1)求滑块与斜面间的动摩擦因数μ;
(2)若使滑块能到达C点,求滑块至少从离地多高处由静止开始下滑;
(3)若滑块离开C处后恰能垂直打在斜面上,求滑块经过C点时对轨道的压力。
【答案】
(1)μ=0.5
(2)H=2m
(3)  N
N
【解析】
试题分析:(1)A到D过程:根据动能定理有
mg(2R-R)- μmgcos45°2R/sin45°=0
可求:μ=0.5
(2)若滑块恰能到达C点,根据牛顿第二定律有:
mg=mvc2/R
从高为H的最高点到C的过程中:根据动能定理有:
mg(H-2R)- μmgcos45°H/sin45°= mvc2/2
求得H=2m
(3)离开C点后滑块做平抛运动,垂直打在斜面上时有
x=v’t
x=v0’t ⑥
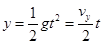 ⑦
⑦
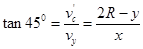 ⑧
⑧
解得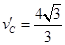 m/s ⑨
m/s ⑨
在C点,有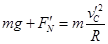 ⑩
⑩
求得: N(=
N(= 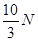 也可以)
也可以)
由牛顿第三定律可知,滑块对轨道的压力为3.3N
考点:本题考查动能定理、平抛运动和牛顿第二定律的应用。

练习册系列答案
相关题目
 (3)金属棒从释放到落地过程中在电子元件上消耗的电能多大?
(3)金属棒从释放到落地过程中在电子元件上消耗的电能多大? 等效电阻
等效电阻 ,式中k为恒量。框架上有一质量为m的金属棒水平放置,金属棒与光滑框架接触良好,离地高为h,磁感应强度为B的匀强磁场与框架平面垂直。将金属棒由静止释放,棒沿框架向下运动。其它电阻不计,问:
,式中k为恒量。框架上有一质量为m的金属棒水平放置,金属棒与光滑框架接触良好,离地高为h,磁感应强度为B的匀强磁场与框架平面垂直。将金属棒由静止释放,棒沿框架向下运动。其它电阻不计,问: (3)金属棒从释放到落地过程中在电子元件上消耗的电能多大?
(3)金属棒从释放到落地过程中在电子元件上消耗的电能多大?

 ,S断开时,电压表示数为16V,S闭合时,电压表示数为10V,若电压表可视为理想的,则电源电动势和内电阻为多少?
,S断开时,电压表示数为16V,S闭合时,电压表示数为10V,若电压表可视为理想的,则电源电动势和内电阻为多少?