题目内容
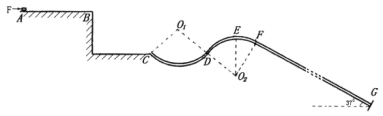
【题目】如图所示，质量
的滑块（可视为质点），在
的水平推力作用下从
点由静止开始运动，一段位移后撤去推力
，当滑块由平台边缘
点飞出后，恰能从
点沿切线方向进入圆弧管道，滑块略小于管道内径。已知
间的距离
，滑块与平台间的动摩擦因数
，、两点间水平距离
、竖直高度差
，
、
是半径均为
的光滑圆弧管道，、
等高，
为管道的最高点，
是长度
、倾角
的粗糙直管道，在
处有一反弹膜，能无机械能损失的反弹滑块，各部分管道在连接处均相切。（
，
）。求：
（1）滑块在平台上运动时水平推力作用的位移大小；
（2）滑块第一次到达点时对轨道的作用力；
（3）要使滑块反弹一次后能停在管道上，滑块与管道之间动摩擦因数的取值范围。
【答案】（1）
；（2）
，方向向上；（3）
【解析】
（1）根据平抛运动
得
由动能定理
得
（2）根据平抛运动
得
从而得
得
根据牛顿第三定律
方向向上
（3）由滑块能停在
上可得
得
由反弹一次可得：
得
分析可得：当时
滑块无法返回
点
综上所述
练习册系列答案
阅读快车系列答案
相关题目
