题目内容
物体沿倾角为θ的斜面下滑,物体与斜面间的滑动摩擦系数为μ,物体的加速度是 .若物体以一定初速度沿此斜面上滑,则加速度是 .
【答案】分析:对物体受力分析,根据牛顿第二定律求出加速度的大小.
解答:解:当物体下滑时,受重力、支持力和沿斜面向上的摩擦力.根据牛顿第二定律得,a=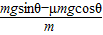 =gsinθ-μgcosθ.
=gsinθ-μgcosθ.
当物体上滑时,受重力、支持力和沿斜面向下的摩擦力,根据牛顿第二定律得,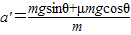 =gsinθ+μgcosθ.
=gsinθ+μgcosθ.
故答案为:g(sinθ-μcosθ),g(sinθ+μcosθ).
点评:解决本题的关键能够正确地受力分析,运用正交分解,根据牛顿第二定律进行求解.
解答:解:当物体下滑时,受重力、支持力和沿斜面向上的摩擦力.根据牛顿第二定律得,a=
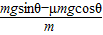 =gsinθ-μgcosθ.
=gsinθ-μgcosθ.当物体上滑时,受重力、支持力和沿斜面向下的摩擦力,根据牛顿第二定律得,
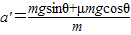 =gsinθ+μgcosθ.
=gsinθ+μgcosθ.故答案为:g(sinθ-μcosθ),g(sinθ+μcosθ).
点评:解决本题的关键能够正确地受力分析,运用正交分解,根据牛顿第二定律进行求解.

练习册系列答案
相关题目
 如图所示,重35N的物体沿倾角为37°的斜面恰好能匀速下滑,物体与斜面间的动摩擦因数μ=
如图所示,重35N的物体沿倾角为37°的斜面恰好能匀速下滑,物体与斜面间的动摩擦因数μ= 如图,一个质量为10kg的物体沿倾角为30°的斜面恰好匀速下滑,现对物体施一水平推力F,使它沿斜面向上匀速运动,求推力F为多大?(g=10N/kg)
如图,一个质量为10kg的物体沿倾角为30°的斜面恰好匀速下滑,现对物体施一水平推力F,使它沿斜面向上匀速运动,求推力F为多大?(g=10N/kg)