题目内容
一个半径为0.5m的飞轮做匀速圆周运动时,每分钟300转,则其边缘上一质量为0.1千克的金属块的线速度为 m/s,向心加速度大小为 m/s2,所受合力大小为 N.
【答案】分析:根据飞轮转速求出飞轮的角速度,再根据飞轮半径求出飞轮边缘金属块的线速度大小和向心加速度大小,再根牛顿第二定律求得金属块所受的合力.
解答:解:根据题意知,飞轮的转速:n=300r/min=5r/s
根据转速与角速度的关系可得:?=2πnrad/s=10πrad/s
所以边缘上的线速度:v=r?=0.5×10πm/s=5πm/s=15.7m/s
根据: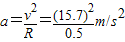 =492.98m/s2
=492.98m/s2
根据牛顿第二定律:F合=ma=0.1×492.98N=49.3N
故答案为:15.7,492.98,49.3
点评:正确理解转速和角速度之间的关系、角速度、半径、和线速度的关系、在匀速圆周运动中合外力提供向心力,根据牛顿第二定律根据向心加速度求出金属块所受的合外力即可.
解答:解:根据题意知,飞轮的转速:n=300r/min=5r/s
根据转速与角速度的关系可得:?=2πnrad/s=10πrad/s
所以边缘上的线速度:v=r?=0.5×10πm/s=5πm/s=15.7m/s
根据:
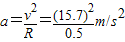 =492.98m/s2
=492.98m/s2根据牛顿第二定律:F合=ma=0.1×492.98N=49.3N
故答案为:15.7,492.98,49.3
点评:正确理解转速和角速度之间的关系、角速度、半径、和线速度的关系、在匀速圆周运动中合外力提供向心力,根据牛顿第二定律根据向心加速度求出金属块所受的合外力即可.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目

