题目内容
 如图,横截面积半径为R的转筒,转筒顶端有一A点,其正下方有一小孔B,距顶端h=0.8m,开始时,转筒的轴线与A点、小孔B三者在同一竖直平面内.现使一小球自A点一速度v=4m/s朝转筒轴线水平抛出,同时转筒立刻以某一角速度匀速转动起来,小球未碰到筒.壁且正好从小孔B穿出,不计空气阻力,g取10m/s2,求:
如图,横截面积半径为R的转筒,转筒顶端有一A点,其正下方有一小孔B,距顶端h=0.8m,开始时,转筒的轴线与A点、小孔B三者在同一竖直平面内.现使一小球自A点一速度v=4m/s朝转筒轴线水平抛出,同时转筒立刻以某一角速度匀速转动起来,小球未碰到筒.壁且正好从小孔B穿出,不计空气阻力,g取10m/s2,求:(1)转筒半径R;
(2)转筒转动的最小角速度取ω;
(3)转筒转动的角速度能否为10πrad/s.
分析:(1)小球做平抛运动,小球穿出小孔,则在平抛运动的时间内的水平位移为2R.
(2)考虑转筒转动的周期性,在平抛运动的时间内,转筒转过的角度为半周的奇数倍.
(2)考虑转筒转动的周期性,在平抛运动的时间内,转筒转过的角度为半周的奇数倍.
解答:解:(1)小球从A点开始做平抛运动,
设小球从A点到进入小孔的时间为t
竖直方向做自由落体运动,h=
gt2①
水平方向做匀速直线运动,
则2R=vt ②
由①、②联立解得
R=0.8 m ③
故转筒半径R为0.8m.
(2)在小球到达小孔的时间t内,圆桶必须恰好转过半周的奇数倍,小球才能钻出小孔
则ωt=(2n+1)π(n=0,1,2…)
由①可得小球到达小孔的时间
t=0.4s
解得ω=(5n+2.5)πrad/s(n=0,1,2…)
所以转筒转动的最小角速度为2.5πrad/s
(3)因为5n+2.5(n=0,1,2…) 不可能取到10
所以ω=(5n+2.5)πrad/s(n=0,1,2…) 不可能等于10πrad/s.
答:(1)转筒半径R为0.8m;
(2)转筒转动的最小角速度为2.5πrad/s;
(3)转筒转动的角速度不能为10πrad/s.
设小球从A点到进入小孔的时间为t
竖直方向做自由落体运动,h=
| 1 |
| 2 |
水平方向做匀速直线运动,
则2R=vt ②
由①、②联立解得
R=0.8 m ③
故转筒半径R为0.8m.
(2)在小球到达小孔的时间t内,圆桶必须恰好转过半周的奇数倍,小球才能钻出小孔
则ωt=(2n+1)π(n=0,1,2…)
由①可得小球到达小孔的时间
t=0.4s
解得ω=(5n+2.5)πrad/s(n=0,1,2…)
所以转筒转动的最小角速度为2.5πrad/s
(3)因为5n+2.5(n=0,1,2…) 不可能取到10
所以ω=(5n+2.5)πrad/s(n=0,1,2…) 不可能等于10πrad/s.
答:(1)转筒半径R为0.8m;
(2)转筒转动的最小角速度为2.5πrad/s;
(3)转筒转动的角速度不能为10πrad/s.
点评:解决本题的关键知道平抛运动在竖直方向上做自由落体运动,在水平方向上做匀速直线运动,以及知道转筒转动的周期性.

练习册系列答案
 优化作业上海科技文献出版社系列答案
优化作业上海科技文献出版社系列答案
相关题目
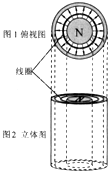 一个足够长的竖直放置的磁铁结构如图所示.在图1中磁铁的两个磁极分别为同心的圆形和圆环形.在两极之间的缝隙中,存在辐射状的磁场,磁场方向水平向外,某点的磁感应强度大小与该点到磁极中心轴的距离成反比.用横截面积一定的细金属丝制成的圆形单匝线圈,从某高度被无初速释放,在磁极缝隙间下落的过程中,线圈平面始终水平且保持与磁极共轴.线圈被释放后( )
一个足够长的竖直放置的磁铁结构如图所示.在图1中磁铁的两个磁极分别为同心的圆形和圆环形.在两极之间的缝隙中,存在辐射状的磁场,磁场方向水平向外,某点的磁感应强度大小与该点到磁极中心轴的距离成反比.用横截面积一定的细金属丝制成的圆形单匝线圈,从某高度被无初速释放,在磁极缝隙间下落的过程中,线圈平面始终水平且保持与磁极共轴.线圈被释放后( )

