题目内容
(10分)如图所示,竖直面内有一绝缘轨道,AB部分是光滑的四分之一圆弧,圆弧半径R=0.5m,B处切线水平,BC部分为水平粗糙直轨道。有一个带负电的小滑块(可视为质点)从A点由静止开始下滑,运动到直轨道上的P处刚好停住。小滑块的质量m=1kg,带电量为 保持不变,滑块小轨道BC部分间的动摩擦因数为μ=0.2,整个空间存在水平向右的匀强电场,电场强度大小为E=4.0×102N/C.(g=10m/s2)
保持不变,滑块小轨道BC部分间的动摩擦因数为μ=0.2,整个空间存在水平向右的匀强电场,电场强度大小为E=4.0×102N/C.(g=10m/s2)
(1)求滑块到达B点前瞬间对轨道的压力大小。
(2)求BP间的距离,
(1)28N(2)
解析试题分析:(1)A→B过程由动能定理  ……2分 解得
……2分 解得 ……1分
……1分
在B处,由牛顿第二定律 ……1分 解得
……1分 解得 ……1分
……1分
由牛顿第三定律:小球对轨道压力  ……1分
……1分
(2)设BP间的距离为S
B→P过程由动能定理 ……2分
……2分
解得: ……2分
……2分
考点:本题考查了动能定理的应用
点评:利用牛顿第二、三定律与运动学公式相结合,同时还运用动能定理,但电场力、重力做功与路径无关,而摩擦力做功与路径有关.

练习册系列答案
 核心素养学练评系列答案
核心素养学练评系列答案 单元期中期末卷系列答案
单元期中期末卷系列答案
相关题目
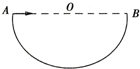 如图所示,竖直面内有一个半圆形轨道,AB为水平直径,O为圆心,将一些半径远小于轨道半径的小球从A点以不同的初速度水平向右抛出,若不计空气阻力,在小球从抛出到碰到轨道这个过程中,下列说法正确的是( )
如图所示,竖直面内有一个半圆形轨道,AB为水平直径,O为圆心,将一些半径远小于轨道半径的小球从A点以不同的初速度水平向右抛出,若不计空气阻力,在小球从抛出到碰到轨道这个过程中,下列说法正确的是( )| A、初速度大的小球运动时间长 | B、小球落到落在半圆形轨道的瞬间,速度方向沿半径方向 | C、落在圆形轨道最低点的小球运动时间最长 | D、初速度不同的小球运动时间不可能相同 |
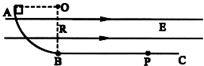 如图所示,竖直面内有一绝缘轨道,AB部分是光滑的四分之一圆弧,圆弧半径R=0.5m,B处切线水平,BC部分为水平粗糙直轨道.有一个带负电的小滑块(可视为质点)从A点由静止开始下滑,运动到直轨道上的P处刚好停住.小滑块的质量m=1kg,带电量为q=-2.5×10-3C保持不变,滑块小轨道BC部分间的动摩擦因数为μ=0.2,整个空间存在水平向右的匀强电场,电场强度大小为E=4.0×102N/C.(g=10m/s2)
如图所示,竖直面内有一绝缘轨道,AB部分是光滑的四分之一圆弧,圆弧半径R=0.5m,B处切线水平,BC部分为水平粗糙直轨道.有一个带负电的小滑块(可视为质点)从A点由静止开始下滑,运动到直轨道上的P处刚好停住.小滑块的质量m=1kg,带电量为q=-2.5×10-3C保持不变,滑块小轨道BC部分间的动摩擦因数为μ=0.2,整个空间存在水平向右的匀强电场,电场强度大小为E=4.0×102N/C.(g=10m/s2) 如图所示,竖直面内有一个半径为R=0.2m的光滑半圆形轨道固定在地面上,水平地面与轨道相切于B点.小球以υ0=3m/s的速度从最低点B进入轨道,关于小球落地点和轨道最低点B的距离,某同学做如下计算:
如图所示,竖直面内有一个半径为R=0.2m的光滑半圆形轨道固定在地面上,水平地面与轨道相切于B点.小球以υ0=3m/s的速度从最低点B进入轨道,关于小球落地点和轨道最低点B的距离,某同学做如下计算: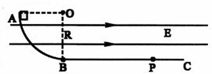 (2009?天津模拟)如图所示,竖直面内有一绝缘轨道,AB部分是光滑的四分之一圆弧,圆弧半径R=0.5m,B处切线水平,BC部分为水平粗糙直轨道.有一个带负电的小滑块(可视为质点)从A点由静止开始下滑,运动到直轨道上的P处刚好停住.小滑块的质量m=1kg,带电量为q=-2.5×10-3C保持不变,滑块小轨道BC部分间的动摩擦因数为μ=0.2,整个空间存在水平向右的匀强电场,电场强度大小为E=4.0×102N/C.(g=10m/s2)
(2009?天津模拟)如图所示,竖直面内有一绝缘轨道,AB部分是光滑的四分之一圆弧,圆弧半径R=0.5m,B处切线水平,BC部分为水平粗糙直轨道.有一个带负电的小滑块(可视为质点)从A点由静止开始下滑,运动到直轨道上的P处刚好停住.小滑块的质量m=1kg,带电量为q=-2.5×10-3C保持不变,滑块小轨道BC部分间的动摩擦因数为μ=0.2,整个空间存在水平向右的匀强电场,电场强度大小为E=4.0×102N/C.(g=10m/s2)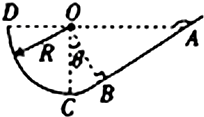 如图所示,竖直面内有一粗糙斜面AB,BCD部分是一个光滑的圆弧面,C为圆弧的最低点,AB正好是圆弧在B点的切线,圈心点O与A、D点在同一高度,∠OAB=37°,圆弧面的半径R=3.6m,一小滑块质量m=5kg,与A斜面间的动摩擦因数μ=0.45,将滑块由A点静止释放,求在以后的运动中(sin37°=0.6,cos37°=0.8)
如图所示,竖直面内有一粗糙斜面AB,BCD部分是一个光滑的圆弧面,C为圆弧的最低点,AB正好是圆弧在B点的切线,圈心点O与A、D点在同一高度,∠OAB=37°,圆弧面的半径R=3.6m,一小滑块质量m=5kg,与A斜面间的动摩擦因数μ=0.45,将滑块由A点静止释放,求在以后的运动中(sin37°=0.6,cos37°=0.8)