题目内容
如图所示，小球由静止开始沿光滑轨道滑下，并沿水平方向抛出，小球抛出后落在斜面上．已知斜面的倾角为θ，斜面上与小球抛出点在同一水平面上，斜面长度为L，斜面上M、N两点将斜面长度等分为3段．小球可以看作质点，空气阻力不计．为使小球能落在M点以上，释放小球的位置相对于抛出点的高度h应满足什么条件？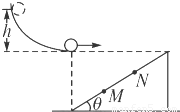
【答案】分析：设小球沿轨道滑至最低点的速度为v，由动能定理列出表达式，小球离开桌面后做平抛运动，若正好落在M点，设运动的时间为t，根据平抛运动特点列式，联立方程即可求解．
解答：解：设小球沿轨道滑至最低点的速度为v，由动能定理得：
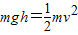①
小球离开桌面后做平抛运动，若正好落在M点，设运动的时间为t：
水平方向有：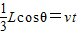
②
竖直方向有：
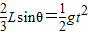③
由①②③解得：
h=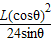
根据题意，要使小球落在M点以上，则h 满足的条件是：h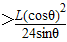
答：要使小球落在M点以上，则h 满足的条件是：h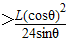
点评：本题主要考查了平抛运动的基本公式及动能定理得直接应用，难度适中．
解答：解：设小球沿轨道滑至最低点的速度为v，由动能定理得：
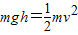①小球离开桌面后做平抛运动，若正好落在M点，设运动的时间为t：
水平方向有：
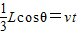②竖直方向有：
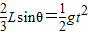③由①②③解得：
h=
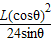
根据题意，要使小球落在M点以上，则h 满足的条件是：h
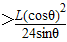
答：要使小球落在M点以上，则h 满足的条件是：h
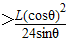
点评：本题主要考查了平抛运动的基本公式及动能定理得直接应用，难度适中．
练习册系列答案
中考解读考点精练系列答案
相关题目
如图所示，小球由静止开始沿光滑轨道滑下，并沿水平方向抛出，小球抛出后落在斜面上．已知斜面的倾角为θ，斜面上与小球抛出点在同一水平面上，斜面长度为L，斜面上M、N两点将斜面长度等分为3段．小球可以看作质点，空气阻力不计．为使小球能落在M点以上，释放小球的位置相对于抛出点的高度h应满足什么条件？
在一根足够长的竖直绝缘杆上，套着一个质量为m、带电量为-q的小球，球与杆之间的动摩擦因数为μ．场强为E的匀强电场和磁感应强度为B的匀强磁场方向如图所示，小球由静止开始下落．小球开始下落时的加速度为
