题目内容
 如图所示,平行金属板长为L,一个带电为+q,质量为m的粒子以初速度v0紧贴上板垂直射入电场,刚好从下板边缘射出,末速度恰与下板成30°角,粒子重力不计.求:
如图所示,平行金属板长为L,一个带电为+q,质量为m的粒子以初速度v0紧贴上板垂直射入电场,刚好从下板边缘射出,末速度恰与下板成30°角,粒子重力不计.求:(1)粒子未速度大小;
(2)电场强度;
(3)两极间距离d.
分析:(1)粒子在电场中做类平抛运动,由运动的合成与分解可知粒子的末速度的大小;
(2)将粒子的运动分解为水平方向的匀速运动和竖直方向的匀加速直线运动,则由运动的合成与分解可求得电场强度;
(3)由动能定理可求得两板间的距离.
(2)将粒子的运动分解为水平方向的匀速运动和竖直方向的匀加速直线运动,则由运动的合成与分解可求得电场强度;
(3)由动能定理可求得两板间的距离.
解答: 解:(1)将末速度分解,
解:(1)将末速度分解,
由几何关系知:
=cos300
所以:v=
;
(2)带电粒子做类平抛运动,依题知,粒子在电场中的运动时间:t=
粒子离开电场时,垂直板方向的分速度:v1=v0tan30°
竖直方向加速度:a=
粒子从射入电场到离开电场,有at=v1
即:
t=v1;
联立以上各式得E=
(3)粒子从射入电场到离开电场,由动能定理,有qEd=
mv2-
m
解得 d=
答:(1)粒子的末速度为
;
(2)电场强度E为
;
(3)板间距离为
.
 解:(1)将末速度分解,
解:(1)将末速度分解,由几何关系知:
| v0 |
| v |
所以:v=
2
| ||
| 3 |
(2)带电粒子做类平抛运动,依题知,粒子在电场中的运动时间:t=
| L |
| v0 |
粒子离开电场时,垂直板方向的分速度:v1=v0tan30°
竖直方向加速度:a=
| Eq |
| m |
粒子从射入电场到离开电场,有at=v1
即:
| Eq |
| m |
联立以上各式得E=
| ||||
| 3qL |
(3)粒子从射入电场到离开电场,由动能定理,有qEd=
| 1 |
| 2 |
| 1 |
| 2 |
| v | 2 0 |
解得 d=
| ||
| 6 |
答:(1)粒子的末速度为
2
| ||
| 3 |
(2)电场强度E为
| ||||
| 3qL |
(3)板间距离为
| ||
| 6 |
点评:带电粒子在电场中的运动,若垂直电场线进入则做类平抛运动,要将运动分解为沿电场线和垂直于电场线两个方向进行分析,利用直线运动的规律进行求解.

练习册系列答案
相关题目
 如图所示,平行金属板长L,间距L,两板间存在向下的匀强电场E,一带电粒子(不计重力)沿两板中线以速度V0垂直射入电场,恰好从下板边缘P点射出平行金属板.若将匀强电场换成垂直纸面的匀强磁场,粒子仍然从同一点以同样的速度射入两板间,要粒子同样从P点射出,求:
如图所示,平行金属板长L,间距L,两板间存在向下的匀强电场E,一带电粒子(不计重力)沿两板中线以速度V0垂直射入电场,恰好从下板边缘P点射出平行金属板.若将匀强电场换成垂直纸面的匀强磁场,粒子仍然从同一点以同样的速度射入两板间,要粒子同样从P点射出,求: (2011?吉安模拟)如图所示,平行金属板A、B带有等量异号电荷,电子和质子均以速率v分别从正(A板)、负(B板)两极板上的小孔沿垂直板面的方向射入板间,那么( )
(2011?吉安模拟)如图所示,平行金属板A、B带有等量异号电荷,电子和质子均以速率v分别从正(A板)、负(B板)两极板上的小孔沿垂直板面的方向射入板间,那么( ) 如图所示,平行金属板与水平方向成θ角,板间距离为d,板间电压为U,一质量为m的带电微粒,以水平初速度v0从下板左端边缘进入板间,结果正好沿水平直线通过从上板右端上边缘处射出,求:
如图所示,平行金属板与水平方向成θ角,板间距离为d,板间电压为U,一质量为m的带电微粒,以水平初速度v0从下板左端边缘进入板间,结果正好沿水平直线通过从上板右端上边缘处射出,求: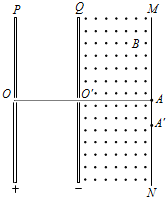 如图所示,平行金属板P、Q的中心分别有小孔O和O′,OO′连线与金属板垂直,两板间的电压为U.在Q板的右侧存在匀强磁场,磁场方向垂直纸面向外,磁感应强度为B.磁场右侧边界处的荧光屏MN与Q板间的距离为L,OO′连线的延长线与MN相交于A点.一质量为m、电荷量为+q的带电粒子,从小孔O处由静止开始运动,通过小孔O′后进入磁场,最终打在MN上的A′点.不计粒子重力.求:
如图所示,平行金属板P、Q的中心分别有小孔O和O′,OO′连线与金属板垂直,两板间的电压为U.在Q板的右侧存在匀强磁场,磁场方向垂直纸面向外,磁感应强度为B.磁场右侧边界处的荧光屏MN与Q板间的距离为L,OO′连线的延长线与MN相交于A点.一质量为m、电荷量为+q的带电粒子,从小孔O处由静止开始运动,通过小孔O′后进入磁场,最终打在MN上的A′点.不计粒子重力.求: 磁流体发电是一项新兴技术,它可以把物体的内能直接转化为电能,如图所示,平行金属板A、B之间相距为d,板间的磁场按匀强磁场处理,磁感应强度为B,等离子体以速度v沿垂直于B的方向射入磁场,金属板A、B是边长为a的正方形,等离子体的电阻率为ρ,外接电阻R.求:
磁流体发电是一项新兴技术,它可以把物体的内能直接转化为电能,如图所示,平行金属板A、B之间相距为d,板间的磁场按匀强磁场处理,磁感应强度为B,等离子体以速度v沿垂直于B的方向射入磁场,金属板A、B是边长为a的正方形,等离子体的电阻率为ρ,外接电阻R.求: