题目内容
 如图所示,固定在小车上的支架的斜杆与竖直杆的夹角为θ,在斜杆下端固定有质量为m的小球,下列关于杆对球的作用力F的判断中,正确的是( )
如图所示,固定在小车上的支架的斜杆与竖直杆的夹角为θ,在斜杆下端固定有质量为m的小球,下列关于杆对球的作用力F的判断中,正确的是( )分析:静止时,球受到重力和杆的弹力,由平衡条件分析弹力的大小和方向.当小车有加速度时,重力和弹力的合力产生加速度,根据牛顿第二定律用合成法求解弹力大小和方向.
解答:解:A、B,小车静止时,球受到重力和杆的弹力,由平衡条件得F=mg,方向:竖直向上.故AB错误.
C、小车向右以加速度a运动时,如图1所示,只有当a=gtanθ时,F=
.故C错误.
D、小车向左以加速度a运动时,如图2所示,根据牛顿第二定 律知小球的合力水平向左,F=
律知小球的合力水平向左,F=
,方向左上方,与竖直方向的夹角为tanα=
.故D正确.
故选D.
C、小车向右以加速度a运动时,如图1所示,只有当a=gtanθ时,F=
| ma |
| sinθ |
D、小车向左以加速度a运动时,如图2所示,根据牛顿第二定
 律知小球的合力水平向左,F=
律知小球的合力水平向左,F=| (ma)2+(mg)2 |
| a |
| g |
故选D.
点评:本题中轻杆与轻绳的模型不同,绳子对物体只有拉力,一定沿绳子方向,而杆子对物体的弹力不一定沿杆子方向,要根据状态,由牛顿定律分析确定.

练习册系列答案
 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案
相关题目
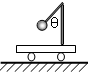 如图所示,固定在小车上的支架的斜杆与竖直杆的夹角为θ,在斜杆下端固定有质量为m的小球,下列关于杆对球的作用力F的判断中,正确的是( )
如图所示,固定在小车上的支架的斜杆与竖直杆的夹角为θ,在斜杆下端固定有质量为m的小球,下列关于杆对球的作用力F的判断中,正确的是( )| A、小车静止时,F=mg,方向竖直向上 | ||
| B、小车静止时,F=mgcosθ,方向垂直杆向上 | ||
| C、小车向右以加速度a运动时,一定有F=ma/sinθ. | ||
D、小车向左以加速度a运动时,F=
|
 如图所示,固定在小车上的支架的斜杆与竖直杆的夹角为θ,在斜杆下端固定有质量为m的小球,下列关于杆对球的作用力F的判断中,正确的是( )
如图所示,固定在小车上的支架的斜杆与竖直杆的夹角为θ,在斜杆下端固定有质量为m的小球,下列关于杆对球的作用力F的判断中,正确的是( ) 如图所示,固定在小车上的折杆∠A=θ,B端固定一个质量为m的小球,若小车向右的加速度为a,AB杆对小球的作用力为F,则( )
如图所示,固定在小车上的折杆∠A=θ,B端固定一个质量为m的小球,若小车向右的加速度为a,AB杆对小球的作用力为F,则( ) 如图所示,固定在小车上的支架的斜杆与竖直杆的夹角为θ,在斜杆下端固定有质量为m的小球,
如图所示,固定在小车上的支架的斜杆与竖直杆的夹角为θ,在斜杆下端固定有质量为m的小球,