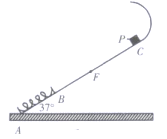
题目内容
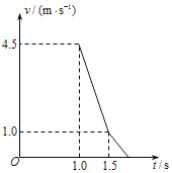
【题目】一长木板在水平地面上运动,从木板经过A点时开始计时,在t=1.0s时将一相对于地面静止的小物块轻放到木板上,此后木板运动的v﹣t图线如图所示.己知木板质量为物块质量的2倍,物块与木板间及木板与地面间均有摩擦,物块与木板间的最大静摩擦力等于滑动摩擦力,且物块始终在木板上,取重力加速度的大小g=10m/s2,求:
(1)物块与木板间的动摩擦因数μ1及木板与地面间的动摩擦因数μ2;
(2)木板离A点的最终距离;
(3)木板的最小长度.
【答案】(1)0.20 0.40 (2)7.975m (3)1.125m
【解析】(1)从![]() 开始,木板与物块之间的摩擦力使物块加速,使木板减速,此过程一直持续到物块和木板具有共同速度为止。
开始,木板与物块之间的摩擦力使物块加速,使木板减速,此过程一直持续到物块和木板具有共同速度为止。
由图可知,在![]() 时,物块和木板具有共同速度
时,物块和木板具有共同速度![]() ,设
,设![]() 到
到![]() 时间间隔内,物块和木板的加速度大小分别为
时间间隔内,物块和木板的加速度大小分别为![]() 和
和![]() ,则有:
,则有:
![]() … ①
… ①![]() … ②
… ②
式中![]() ,为木板在
,为木板在![]() 时速度的大小。
时速度的大小。
设物块和木板的质量分别为m、2m,由牛顿第二定律得:![]() …③
…③
![]() …④
…④
联立①②③④式得: ![]() ,
, ![]()
(2)设![]() 到
到![]() 时间间隔内,木板的加速度为
时间间隔内,木板的加速度为![]() ,由牛顿第二定律得:
,由牛顿第二定律得: ![]() …⑤
…⑤
得: ![]()
逆过来看,将木板匀减速过程看作反向匀加速过程,则![]() 到
到![]() 时间间隔内木板的位移为:
时间间隔内木板的位移为: ![]() … ⑥
… ⑥
代入数据解得: ![]()
![]() 到
到![]() 时间间隔内,木板相对于地面的运动距离为:
时间间隔内,木板相对于地面的运动距离为: ![]() … ⑦
… ⑦
代入数据解得: ![]()
在![]() 时刻后,地面对木板的摩擦力阻碍木板运动,物块与木板之间的摩擦力改变方向。设物块与木板之间的摩擦力大小为
时刻后,地面对木板的摩擦力阻碍木板运动,物块与木板之间的摩擦力改变方向。设物块与木板之间的摩擦力大小为![]() ,物块和木板的加速度大小分别为
,物块和木板的加速度大小分别为![]() 和
和![]() ,则由牛顿第二定律得:
,则由牛顿第二定律得: ![]() …⑧
…⑧
![]() …⑨
…⑨
假设![]() ,则
,则![]() ;
;
由⑧⑨式得![]() ,与假设矛盾,故有:
,与假设矛盾,故有: ![]() …⑩
…⑩
由⑨⑩式得: ![]() ,
, ![]()
在![]() 时刻后,木板相对于地面的运动距离为:
时刻后,木板相对于地面的运动距离为: ![]()
代入数据解得: ![]()
综上,木板离A点的最终距离![]()
解得: ![]()
(3)由(2)分析,物块的![]() 图象如图中点划线所示。由图可知,
图象如图中点划线所示。由图可知, ![]() 到
到![]() 时间间隔内,物块相对于木板的位移逐渐增大,而
时间间隔内,物块相对于木板的位移逐渐增大,而![]() 时刻后,物块相对于木板的位移又逐渐减小。
时刻后,物块相对于木板的位移又逐渐减小。![]() 到
到![]() 时间间隔内,物块相对于地面的运动距离为
时间间隔内,物块相对于地面的运动距离为
![]()
代入数据解得 ![]()
木板的最小长度应等于物块相对于木板的最大位移的大小,为: ![]()
解得![]() 。
。