题目内容
某高速公路转弯处，弯道半径R=100m，汽车轮胎与路面问的动摩擦因数为μ=0.8，路面要向圆心处倾斜，汽车若以v=15m/s的速度行驶时．
（1）在弯道上没有左右滑动趋势，则路面的设计倾角θ应为多大（求出θ的某个三角函数值即可）？
（2）若θ=37°，汽车的质量为2000kg，当汽车的速度为30m/s时车并没有发生侧向滑动，求此时地面对汽车的侧向摩擦力的大小和方向．（g=10m/s2，sin37°=0.6）
解：（1）汽车转弯时由牛顿第二定律得：mgtanθ=m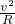
得tanθ=
=0.225
（2）若汽车所受侧向摩擦力沿斜面向里，对汽车进行受力分析，如图所示：
由正交分解得
f+mgsinθ=macosθ
a=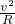=9m/s2
解方程得f=2400N，说明侧向摩擦力沿斜面向里．
答：（1）在弯道上没有左右滑动趋势，则路面的设计倾角θ应为tanθ=0.225（求出θ的某个三角函数值即可）；
（2）此时地面对汽车的侧向摩擦力的大小为2400N，方向沿斜面向里．
分析：（1）在弯道上没有左右滑动趋势，则说明仅靠重力的分量提供向心力，根据向心力公式即可求解；
（2）可先假设汽车所受侧向摩擦力沿斜面向里，先求出此时汽车的加速度，再对汽车进行受力分析即可求解．
点评：熟记向心力公式是解决本题的关键，弄清向心力是由哪些力提供的，通常这样找向心力：沿半径方向的所有力的合力提供该物体做圆周运动的向心力．
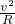
得tanθ=
=0.225（2）若汽车所受侧向摩擦力沿斜面向里，对汽车进行受力分析，如图所示：
由正交分解得
f+mgsinθ=macosθ
a=
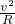=9m/s2解方程得f=2400N，说明侧向摩擦力沿斜面向里．
答：（1）在弯道上没有左右滑动趋势，则路面的设计倾角θ应为tanθ=0.225（求出θ的某个三角函数值即可）；
（2）此时地面对汽车的侧向摩擦力的大小为2400N，方向沿斜面向里．
分析：（1）在弯道上没有左右滑动趋势，则说明仅靠重力的分量提供向心力，根据向心力公式即可求解；
（2）可先假设汽车所受侧向摩擦力沿斜面向里，先求出此时汽车的加速度，再对汽车进行受力分析即可求解．
点评：熟记向心力公式是解决本题的关键，弄清向心力是由哪些力提供的，通常这样找向心力：沿半径方向的所有力的合力提供该物体做圆周运动的向心力．
练习册系列答案
寒假天地重庆出版社系列答案
相关题目
图a用铁架台、弹簧和多个已知质量且质量相等的钩码，探究在弹性限度内弹簧弹力与弹簧伸长长度的关系实验
如图所示，倾角为θ=37°的光滑斜面AB长为L=48m，底端有一小段光滑圆弧与光滑水平面BC相连，质量为m=0.4kg的物体，从斜面顶端静止起沿斜面下滑，求：（sin37°=0.6）
，A便开始向右运动，并与B发生多次对心碰撞，碰撞过程时间极短，每次碰撞后两物体交换速度，A带电量不变，B始终不带电．g取10m/s2
某同学探究弹力与弹簧伸长量的关系．
（1）将弹簧悬挂在铁架台上，将刻度尺固定在弹簧一侧．弹簧轴线和刻度尺都应在______方向（填“水平”或“竖直”）．
（2）弹簧自然悬挂，待弹簧______时，长度记为L0；弹簧下端挂上砝码盘时，长度记为Lx；在砝码盘中每次增加10g砝码，弹簧长度依次记为L1至L6，数据如下表：
| 代表符号 | L0 | Lx | L1 | L2 | L3 | L4 | L5 | L6 |
| 数值[cm] | 25.35 | 27.35 | 29.35 | 31.30 | 33.4 | 35.35 | 37.40 | 39.30 |
（3）如图是该同学根据表中数据作的图，纵轴是砝码的质量，横轴是弹簧长度与______的差值（填“L0”或“Lx”）．
（4）由图可知弹簧的劲度系数为______N/m；通过图和表可知砝码盘的质量为______g（结果保留两位有效数字，重力加速度取9.8m/s2）．
如图所示，一个小物块在固定的斜面上匀速下滑．关于小物块的受力情况，下列说法中正确的是
如图所示，整个装置处于平衡状态，左右两段轻线与天花板所成的角度分别为45°和60°，中间一段轻线水平，则悬于轻线上两个物体的质量m1________m2（填大于、等于或小于）；质量之比m1：m2=________．
在倾角为θ的长斜面上有一带风帆的滑块，从静止开始沿斜面下滑．滑块质量为m，它与斜面间的动摩擦因数为μ，帆受到的空气阻力与帆的受风面积s以及滑块下滑速度v的大小成正比，即f=ksv．