题目内容
 如图所示,两个轮子相互咬合而转动,对轮上的a、b、c三点,以下正确的是( )
如图所示,两个轮子相互咬合而转动,对轮上的a、b、c三点,以下正确的是( )| A、a的角速度与c的角速度相同 | B、a的线速度与c的线速度大小相等 | C、b的角速度与c的角速度相等 | D、b的线速度与c的线速度相等 |
分析:咬后的两齿轮有两轮边缘上线速度大小相等,根据线速度大小相等和各物理量的关系求解即可.由于同轴转动,轮上各个点的角速度相同(圆心除外),故三点的角速度相同,再根据线速度与角速度的关系式求解.注意:线速度是矢量.
解答:解:A、根据题意有两轮边缘上的线速度大小相等,即有va=vc,根据角速度ω和线速度v的关系v=rω得,角速度与半径成反比,a的角速度大于c的角速度,故A错误,B正确;
B、由于同轴转动,轮上各个点的角速度相同(圆心除外),故b的角速度与c的角速度相同,据V=ωr知:c的线速度大小大于b的线速度,故C正确,D错误.
故选:BC.
B、由于同轴转动,轮上各个点的角速度相同(圆心除外),故b的角速度与c的角速度相同,据V=ωr知:c的线速度大小大于b的线速度,故C正确,D错误.
故选:BC.
点评:抓住齿轮咬合传动时,两轮边缘上线速度大小相等展开讨论,同轴转动,角速度相同是解决本题的关键.熟练掌握描述圆周运动的各物理量之间的关系是解决本题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
向心力演示器如图所示。转动手柄1,可使变速塔轮2和3以及长槽4和短槽5随之匀速转动,槽内的小球就做匀速圆周运动。小球做圆周运动的向心力由横臂6的挡板对小球的压力提供,球对挡板的反作用力通过横臂的杠杆使弹簧测力套筒7下降,从而露出标尺8,标尺8上露出的红白相间等分格子的多少可以显示出两个球所受向心力的大小。皮带分别套在塔轮2和3上的不同圆盘上,可改变两个塔轮的转速比,以探究物体做圆周运动的向心力大小跟哪些因素有关、具体关系怎样。现将小球A和B分别放在两边的槽内,小球A和B的质量分别为mA和mB,做圆周运动的半径分别为rA和rB。皮带套在两塔轮半径相同的两个轮子上,实验现象显示标尺8上左边露出的等分格子多于右边,则下列说法正确的( )
| A.若rA>rB,mA=mB,说明物体的质量和角速度相同时,半径越大向心力越大 |
| B.若rA>rB,mA=mB,说明物体的质量和线速度相同时,半径越大向心力越大 |
| C.若rA=rB,mA≠mB,说明物体运动的半径和线速度相同时,质量越大向心力越小 |
| D.若rA=rB,mA≠mB,说明物体运动的半径和角速度相同时,质量越大向心力越小 |
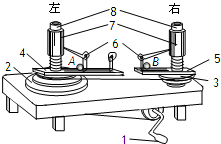 (2011?海淀区模拟)向心力演示器如图所示.转动手柄1,可使变速塔轮2和3以及长槽4和短槽5随之匀速转动,槽内的小球就做匀速圆周运动.小球做圆周运动的向心力由横臂6的挡板对小球的压力提供,球对挡板的反作用力通过横臂的杠杆使弹簧测力套筒7下降,从而露出标尺8,标尺8上露出的红白相间等分格子的多少可以显示出两个球所受向心力的大小.皮带分别套在塔轮2和3上的不同圆盘上,可改变两个塔轮的转速比,以探究物体做圆周运动的向心力大小跟哪些因素有关、具体关系怎样.现将小球A和B分别放在两边的槽内,小球A和B的质量分别为mA和mB,做圆周运动的半径分别为rA和rB.皮带套在两塔轮半径相同的两个轮子上,实验现象显示标尺8上左边露出的等分格子多于右边,则下列说法正确的( )
(2011?海淀区模拟)向心力演示器如图所示.转动手柄1,可使变速塔轮2和3以及长槽4和短槽5随之匀速转动,槽内的小球就做匀速圆周运动.小球做圆周运动的向心力由横臂6的挡板对小球的压力提供,球对挡板的反作用力通过横臂的杠杆使弹簧测力套筒7下降,从而露出标尺8,标尺8上露出的红白相间等分格子的多少可以显示出两个球所受向心力的大小.皮带分别套在塔轮2和3上的不同圆盘上,可改变两个塔轮的转速比,以探究物体做圆周运动的向心力大小跟哪些因素有关、具体关系怎样.现将小球A和B分别放在两边的槽内,小球A和B的质量分别为mA和mB,做圆周运动的半径分别为rA和rB.皮带套在两塔轮半径相同的两个轮子上,实验现象显示标尺8上左边露出的等分格子多于右边,则下列说法正确的( )

