题目内容
（2011?安徽模拟）如图所示，在倾角θ=37°的固定斜面上放置一质量M=1kg、长度L=3m的薄平板AB．平板的上表面光滑，其下端B与斜面底端C的距离为7m．在平板的上端A处放一质量m=0.6kg的滑块，开始时使平板和滑块都静止，之后将它们无初速释放．设平板与斜面间、滑块与斜面间的动摩擦因数均为μ=0.5，求滑块与平板下端B到达斜面底端C的时间差△t．（sin37°=0.6，cos37°=0.8，g=10m/s2）分析：分别研究滑块与平板的运动情况：开始时，由于Mgsin37°＜μ（M+m）gcos37°，滑块在平板上滑动时，平板静止不动．根据牛顿第二定律求出滑块的加速度，由位移-速度关系式求出滑块到达B点时的速度．滑块离开平板后，根据牛顿第二定律求出滑块沿斜面下滑的加速度，由位移公式求解滑块由B至C所用时间．滑块滑离后平板才开始运动，根据牛顿第二定律求出平板沿斜面下滑的加速度，由位移公式求解滑块由B至C所用时间．再求解时间差．
解答：解：对平板，由于Mgsin37°＜μ（M+m）gcos37°，故滑块在平板上滑动时，平板静止不动．
对滑块：在薄板上滑行时加速度a1=gsin37°=6m/s2，到达B点时速度
v=
=6m/s
滑块由B至C时的加速度a2=gsin37°-μgcos37°=2m/s2，设滑块由B至C所用时间为t，
则LBC=vt+
a2t2，
代入解得t=1s
对平板，滑块滑离后才开始运动，加速度a=gsin37°-μgcos37°=2m/s2，设滑至C端所用
时间为t'，则
LBC=
at′2，解得t′=
s
滑块与平板下端B到达斜面底端C的时间差为
△t=t′-t=(
-1)s=1.65s
答：滑块与平板下端B到达斜面底端C的时间差△t=1.65s．
对滑块：在薄板上滑行时加速度a1=gsin37°=6m/s2，到达B点时速度
v=
| 2a1L |
滑块由B至C时的加速度a2=gsin37°-μgcos37°=2m/s2，设滑块由B至C所用时间为t，
则LBC=vt+
| 1 |
| 2 |
代入解得t=1s
对平板，滑块滑离后才开始运动，加速度a=gsin37°-μgcos37°=2m/s2，设滑至C端所用
时间为t'，则
LBC=
| 1 |
| 2 |
| 7 |
滑块与平板下端B到达斜面底端C的时间差为
△t=t′-t=(
| 7 |
答：滑块与平板下端B到达斜面底端C的时间差△t=1.65s．
点评：本题关键在于分析两物体的受力情况，再确定物体的运动情况．也可以运用动能定理与运动学公式结合求解．
练习册系列答案
相关题目
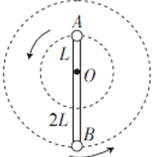（2011?安徽模拟）如图所示，轻杆长为3L，在杆的A、B两端分别固定质量均为m的球A和球B，杆上距球A为L处的点O装在光滑的水平转动轴上，外界给予系统一定的能量后，杆和球在竖直面内转动．在转动的过程中，忽略空气的阻力．若球B运动到最高点时，球B对杆恰好无作用力，则下列说法正确的是（ ）
（2011?安徽模拟）如图所示为大型电子地磅电路图，电源电动势为E，内阻不计．不称物体时，滑片P到A端，滑动变阻器接入电路的有效电阻最大，电流较小；称重物时，在压力作用下使滑片P下滑，滑动变阻器有效电阻变小，电流变大，这样把电流对应的重量值刻在刻度盘上，就可以读出被称物体的重量值，若滑动变阻器上A、B间距离为L，最大阻值等于电阻阻值R0，已知两只弹簧的总弹力与形变量成正比，其比例系为k，所称重物的重量G与电流大小I的关系为（ ）
（2011?安徽模拟）如图所示，有一足够长斜面，倾角α=37°，一小物块质量为m，从斜面顶端A处由静止下滑，到B处后，受一与物体重力大小相等的水平向右恒力作用，开始减速，到C点减速到0（C点未画出）．若AB=225m．物块与斜面间动摩擦因素μ=0.5，sin37°=0.6，cos37°=0.8，g=10m/s2．
（2011?安徽模拟）如图是某中学科技小组制作的利用太阳能驱动小车的装置．当太阳光照射到小车上方的光电板，光电板中产生的电流经电动机带动小车前进．若射到小车上方的光电板，光电板中产生的电流经电动机带动小车前进．若小车在平直的水泥路上从静止开始加速行驶，经过时间t前进距离s，速度达到最大值vm，设这一过程中电动机的功率恒为P，小车所受阻力恒为F，那么（ ）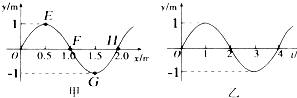
（2011?安徽模拟）一列沿着x轴正方向传播的横波，在t=2s时刻的波形如图甲所示，则图乙表示图甲中E、F、G、H四个质点中，哪一质点的振动图象（ ）