题目内容
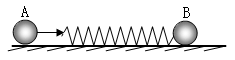
 光滑地面上放着两钢球A和B,且mA<mB,B上固定着一轻弹簧,如图所示,现在A以速率v0碰撞静止的B球,有( )
光滑地面上放着两钢球A和B,且mA<mB,B上固定着一轻弹簧,如图所示,现在A以速率v0碰撞静止的B球,有( )| A、当弹簧压缩量最大时,A、B两球的速率都最小 | B、当弹簧恢复原长时,A球速率为零 | C、当A球速率为零时,B球速率最大 | D、当B球速率最大时,弹簧的势能为零 |
分析:两球与弹簧正常的系统动量守恒,机械能守恒,分析球的运动过程,应用动量守恒定律与机械能守恒定律分析答题.
解答:解:A、A与弹簧接触后,弹簧被压缩,A做减速运动,B做加速运动,弹簧压缩量最大时,A、B速度相等,然后A继续做减速运动,B继续做加速运动,因此弹簧压缩量最大时,A球的速率不是最小,故A错误;
B、设弹簧恢复原长时,弹簧弹性势能为零,A的速度为vA,B的速度为vB,A、B、弹簧组成的系统为研究对象,系统动量守恒,机械能守恒,以A的初速度方向为正方向,由动量守恒定律得:mAv0=mAvA+mBvB,由能量守恒定律得:
mAv02=
mAvA2+
mBvB2,解得:vA=
v0,由于mA<mB,vA=
v0<0,A的速度方向与初速度方向相反,水平向左,A的速度不为零,故B错误;
C、弹簧压缩量最大时,A、B两球速度相等,然后A继续做减速运动,B做加速运动,当弹簧恢复原长时,B的速度最大,由B可知,在弹簧恢复原长时,A的速度向左,因此在弹簧恢复原长前某时刻,A的速度为零,此时B球速度小于弹簧恢复原长时B的速度,B的速度没有达到最大,故C错误;
D、由C的分析可知,当弹簧恢复原长时,B的速度最大,此时弹簧的弹性势能为零,故D正确;
故选:D.
B、设弹簧恢复原长时,弹簧弹性势能为零,A的速度为vA,B的速度为vB,A、B、弹簧组成的系统为研究对象,系统动量守恒,机械能守恒,以A的初速度方向为正方向,由动量守恒定律得:mAv0=mAvA+mBvB,由能量守恒定律得:
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| mA-mB |
| mA+mB |
| mA-mB |
| mA+mB |
C、弹簧压缩量最大时,A、B两球速度相等,然后A继续做减速运动,B做加速运动,当弹簧恢复原长时,B的速度最大,由B可知,在弹簧恢复原长时,A的速度向左,因此在弹簧恢复原长前某时刻,A的速度为零,此时B球速度小于弹簧恢复原长时B的速度,B的速度没有达到最大,故C错误;
D、由C的分析可知,当弹簧恢复原长时,B的速度最大,此时弹簧的弹性势能为零,故D正确;
故选:D.
点评:分析清楚运动过程是正确解题的前提与关键,分析清楚运动过程、应用动量守恒定律与能量守恒定律即可正确解题.

练习册系列答案
相关题目